Third-Polarizing-Filter Experiment Demystified — How It Works
© Copyright 2004 Darel Rex Finley. All rights reserved. This article, with illustrations and copyright notice intact, may be freely distributed for educational purposes.
Shine light through two polarizing filters oriented at 90° to each other, and no light gets through. But put a third filter inbetween them, at 45° to each of the existing filters, and amazingly enough — some lights gets through!
This popular experiment is often described as “strange.” It is usually presented in the context of quantum mechanics, as an example of the “spookiness” of quantum effects. Rarely, however, does the presenter inform the audience that this experiment can be explained in very simple terms of cause and effect, without reference to spooky quantum magic or anything like that.
Let’s start by going over the standard experiment:
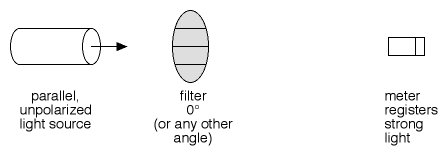
Figure 1
In Figure 1, an unpolarized, parallel light source is fired through a polarizing filter, and the light strongly registers in a light meter at the other end.
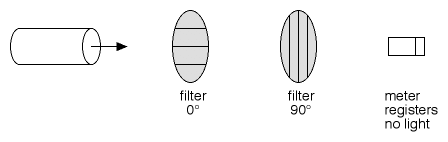
Figure 2
In Figure 2, a second filter is introduced, oriented at 90° to the first one. Now, no light gets through.
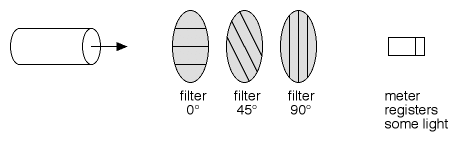
Figure 3
In Figure 3, a third filter is placed inbetween the first two, at 45° to each of them. Suddenly, the light meter registers a significant amount of light, although not as much as in Figure 1. Spooky!
Spookiness and the Word “Filter”
Why do these results seem spooky? The reason is because of the misapplication of the word “filter.” A filter is commonly understood to mean a device that knocks some items out of a stream, while leaving others essentially untouched. A good example of a filter is a sieve — it blocks objects of a particular size, while allowing objects of other sizes to pass through.
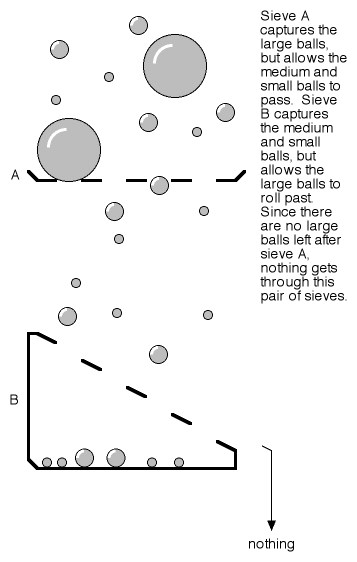
Figure 4
Another example would be a color filter that knocks out some frequencies of light while letting others through.
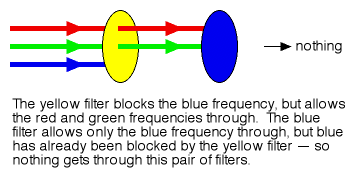
Figure 5
Understood this way, the results of the polarizer experiment are indeed spooky. If the all-blocking equivalent of Figure 2 is constructed using sieves or color frequency filters (see Figures 4 and 5), we are certainly confident that the addition of more filters in the middle of the sequence will not yield different results at the end.
But what if our so-called “filters” could not only block components of the stream, but also change them? Then we would not be surprised at all if the addition of new “filters” in the middle caused items to get through to the end. If a sieve could not only block particles, but also change their size, or if a color filter could not only block frequencies, but shift light to a different frequency, then all bets are off.
This, in fact, is what a polarizer does.
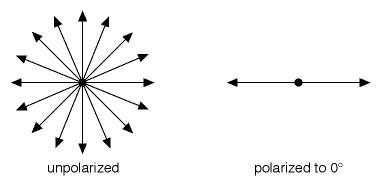
Figure 6
Look at Figure 6 and ask yourself this question: What percentage of the unpolarized light is oriented to exactly 0° or very nearly 0°? Almost none of it — certainly less than 1%. So, if a polarizer simply knocked out undesirable orientations, the strength of the remaining light would be almost entirely gone — it would be less than 1% as strong as the original light source. But you know a polarizer doesn’t do that, because you can pick up an ordinary pair of polarizing sunglasses and observe that they’re not even particularly dark! Obviously, something else must be happening.

Figure 7
Let’s see what happens to each of the orientations represented in our simple diagram (from Figure 6):

Figure 8
In Figure 8, we see that light already at 0° is unchanged. We knew that already.
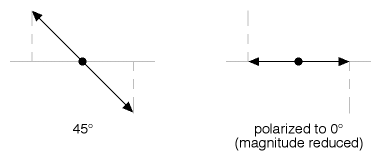
Figure 9
In Figure 9, we see what happens to light oriented at 45° — it has its transverse (vertical) component destroyed, and becomes oriented to 0°, but with a weaker magnitude. Simple geometry tells us that it must have a magnitude about 71% of what it had before being polarized to 0° — i.e., 1/sqrt(2) = .707
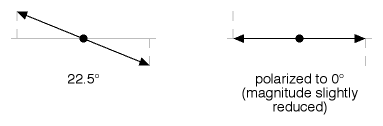
Figure 10
Figure 10 shows us that light that is close to 0° loses only a little of its magnitude when being crushed to 0°...
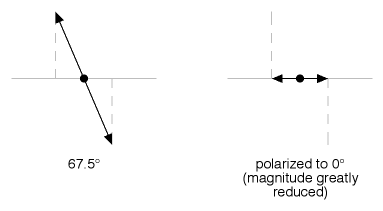
Figure 11
...while Figure 11 shows us that light that is close to 90° off of the polarizer loses most of its magnitude when being crushed to 0°.
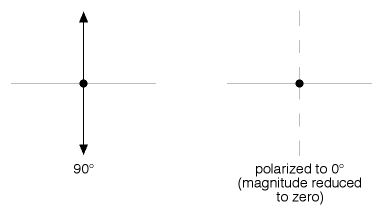
Figure 12
And finally, Figure 12 illustrates light at 90° to the filter being crushed completely out of existence. Figure 12, in fact, illustrates what is happening in Figure 2 when we had only two polarizers in the path of our light source.
What is happening in Figure 3? With our new understanding of what a polarizer does, it is easy to figure it out:
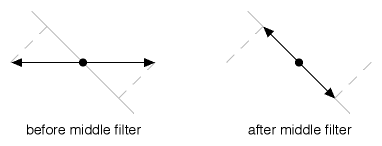
Figure 13
Figure 13 shows the middle filter taking 0° polarized light (from the first filter) and crushing it to a 45° orientation. This causes the light to drop to about 71% of its magnitude coming from the first filter.
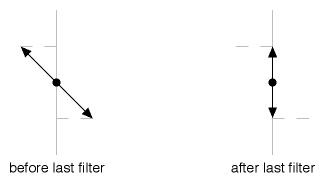
Figure 14
And Figure 14 shows the last filter taking the 45° polarized light (from the middle filter) and crushing it to a 90° orientation. This causes another 29% drop (0.71x) in magnitude, for an overall drop of exactly 50% (as compared to the results of the single-filter setup in Figure 1). These results can be verified by performing the experiment with an actual light meter — the meter should show about twice as strong a reading in the Figure 1 arrangement as it does in the Figure 3 arrangement.
So there you have it! No spooky quantum properties. Nothing very mysterious about it, in fact. A straightforward chain of cause and effect, yielding rational, comprehensible results.
Send me an e-mail!
Quicksort |
Point-in-polygon |
Mouseover menus |
Gyroscope |
Osmosis |
Polarizer experiment |
Calculus without calculus |
Overlapping maze














