Inset A Polygon By A Fixed, Perpendicular Distance, With C Code Sample
© 2007 Darel Rex Finley.  This complete article, unmodified, may be freely distributed for educational purposes.





Suppose you have a polygon like the black one above. How do you create a polygon like the blue one, that is inset by a fixed distance (red) from every side of the black polygon?  The key is figuring out how to inset each corner of the polygon so that the new sides are exactly the right distance from the old sides.  To do that, we will offset each side by the desired distance, then find the point where they intersect, like so:



If the two sides do not intersect, extend them as far as necessary until they do:



If the two sides are colinear, they have no real intersection point, so we will just use the point where they meet:




C Code Sample

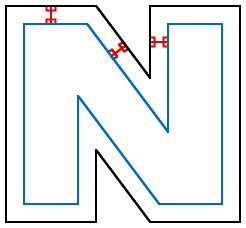
//  public-domain code by Darel Rex Finley, 2007 //  See diagrams at http://alienryderflex.com/polygon_inset void insetPolygon(double *x, double *y, int corners, double insetDist) {   double  startX=x[0], startY=y[0], a, b, c, d, e, f ;   int     i ;   //  Polygon must have at least three corners to be inset.   if (corners<3) return;   //  Inset the polygon.   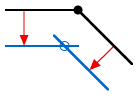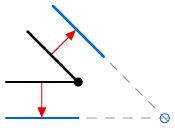c=x[corners-1]; d=y[corners-1]; e=x[0]; f=y[0];   for (i=0; i<corners-1; i++) {     a=c; b=d; c=e; d=f; e=x[i+1]; f=y[i+1];     insetCorner(a,b,c,d,e,f,&x[i],&y[i],insetDist); }   insetCorner(c,d,e,f,startX,startY,&x[i],&y[i],insetDist); } //  Given the sequentially connected points (a,b), (c,d), and (e,f), this //  function returns, in (C,D), a bevel-inset replacement for point (c,d). 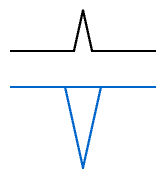// //  Note:  If vectors (a,b)->(c,d) and (c,d)->(e,f) are exactly 180° opposed, //         or if either segment is zero-length, this function will do //         nothing; i.e. point (C,D) will not be set. void insetCorner( double  a, double  b,   //  previous point double  c, double  d,   //  current point that needs to be inset double  e, double  f,   //  next point double *C, double *D,   //  storage location for new, inset point double insetDist) {     //  amount of inset (perpendicular to each line segment)   double  c1=c, d1=d, c2=c, d2=d, dx1, dy1, dist1, dx2, dy2, dist2, insetX, insetY ;   //  Calculate length of line segments.   dx1=c-a; dy1=d-b; dist1=sqrt(dx1*dx1+dy1*dy1);   dx2=e-c; dy2=f-d; dist2=sqrt(dx2*dx2+dy2*dy2);   //  Exit if either segment is zero-length.   if (dist1==0. || dist2==0.) return;   //  Inset each of the two line segments.   insetX= dy1/dist1*insetDist; a+=insetX; c1+=insetX;   insetY=-dx1/dist1*insetDist; b+=insetY; d1+=insetY;   insetX= dy2/dist2*insetDist; e+=insetX; c2+=insetX;   insetY=-dx2/dist2*insetDist; f+=insetY; d2+=insetY;   //  If inset segments connect perfectly, return the connection point.   if (c1==c2 && d1==d2) {     *C=c1; *D=d1; return; }   //  Return the intersection point of the two inset segments (if any).   if (lineIntersection(a,b,c1,d1,c2,d2,e,f,&insetX,&insetY)) {     *C=insetX; *D=insetY; }}

This code is not significantly disturbed by polygons that include colinear switchbacks — it just won’t inset the points that can’t be inset.  However, polygons that have narrow pieces that don’t leave enough room for inset will give wierd results that don’t look line a polygon inset, for example:



Clockwise vs. counterclockwise

The above code is written to work correctly on a clockwise-traced polygon.  If the polygon is traced counterclockwise, the new polygon will be outset — for example, the blue polygon at the top of this article would become the black one.  You can also outset a polygon by passing a negative value in insetDist.  And, if your polygon is traced counterclockwise, you can inset it by passing a negative value in insetDist.


Send me an e-mail!

Does the brace style in the above code sample freak you out?  Click here to see it explained in a new window.

Back to tutorials.