Perimeter of A Complex Polygon, With C Code Sample

Perimeter of A Complex Polygon, With C Code Sample
© 2007 Darel Rex Finley. This complete article, unmodified, may be freely distributed for educational purposes.

This page addresses the problem of tracing the outside edge (perimeter) of a complex (i.e. self-crossing) polygon, in a consistently clockwise direction. Obtaining such a perimeter polygon is useful for filling the polygon without leaving any overlap areas unfilled, or for calculating the total area of the polygon without any negative areas, non-counted areas, or multiply-counted areas.

Here’s how we do it:

1. Reformulate the polygon as a set of line segments, each with its own startpoint and endpoint (i.e. not a list of sequentially connected corners). In this illustration, each line segment is given a different color:

2. Break all the segments up at their intersection points, so that the resultant set of segments includes no crossing segments. In this illustration, each of the new segments is given a different color — notice that they connect with each other at their endpoints, but do not cross each other as they did in the previous illustration:

3. Choose a starting point that must be on the perimeter. We will use the point with the largest Y-coordinate (the highest point), and if more than one point shares the largest Y-coordinate, then the one with the smallest X-coordinate (the leftmost) of those will be used. We will also draw an imaginary horizontal segment extending directly to the left (toward the negative X direction) from that starting point, and pretend that this segment is the last segment we have chosen, for purposes of beginning the procedure described in step 4 below:

4. Build the perimeter polygon by iteratively choosing whichever connecting segment veers leftmost from the last segment’s endpoint — i.e. the one that has the smallest clockwise angle from the previously chosen segment:

Pretty simple, huh? But coding it is an ugly chore. Save yourself the trouble and use this sample:

C Code Sample

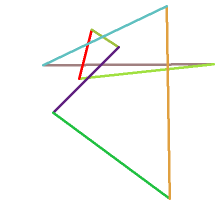
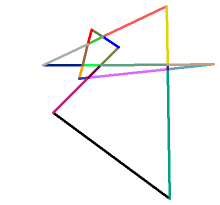
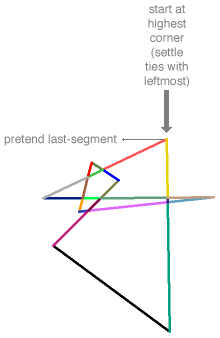
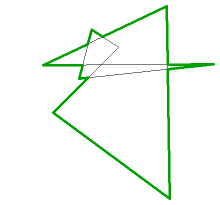
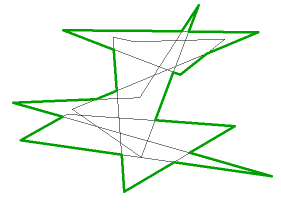
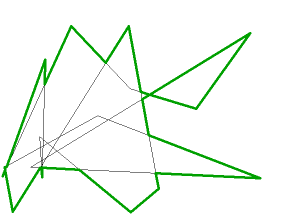
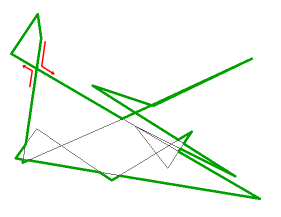
//  public-domain code by Darel Rex Finley, 2007

//  See examples at http://alienryderflex.com/polygon_perimeter







#include <math.h>







#define  CIRCLE_RADIANS     6.283185307179586476925286766559

#define  MAX_SEGS        1000







//  Determine the radian angle of the specified point (as it relates to the

//  origin).

//

//  Warning:  Do not pass zero in both parameters, as this will cause a division-

//            by-zero.



double angleOf(double x, double y) {



  double  dist=sqrt(x*x+y*y) ;



  if (y>=0.) return acos( x/dist);

  else       return acos(-x/dist)+.5*CIRCLE_RADIANS; }







//  Returns the perimeter polygon in newX and newY (which must have at least

//  MAX_SEGS elements each to prevent the possibility of overrun).  "corners" is

//  used to pass in the size of the original polygon, and to return the size of

//  the new, perimeter polygon.

//

//  If for any reason the procedure fails, it will return NO in its bool return

//  value, in which case the values in "newX", "newY", and "corners" should not

//  be trusted.



bool polygonPerimeter(

double *x, double *y, int *corners, double *newX, double *newY) {



  double  segSx[MAX_SEGS], segSy[MAX_SEGS], segEx[MAX_SEGS], segEy[MAX_SEGS] ;

  double  segAngle[MAX_SEGS], intersectX, intersectY ;

  double  startX=x[0], startY=y[0], lastAngle=.5*CIRCLE_RADIANS, turnAngle ;

  double  a, b, c, d, e, f, angleDif, bestAngleDif ;

  int     i, j=(*corners)-1, segs=0 ;



  if ((*corners)>MAX_SEGS) return NO;



  //  1,3.  Reformulate the polygon as a set of line segments, and choose a

  //        starting point that must be on the perimeter.

  for (i=0; i<(*corners); i++) {

    if (x[i]!=x[j] || y[i]!=y[j]) {

      segSx[segs]=x[i]; segSy[segs]=y[i]; segEx[segs]=x[j]; segEy[segs++]=y[j]; }

    j=i;

    if (y[i]>startY || y[i]==startY && x[i]<startX) {

      startX=x[i]; startY=y[i]; }}

  if (segs==0) return NO;



  //  2.  Break the segments up at their intersection points.

  for   (i=  0; i<segs-1; i++) {

    for (j=i+1; j<segs  ; j++) {

      if
(lineSegmentIntersection(

      segSx[i],segSy[i],segEx[i],segEy[i],

      segSx[j],segSy[j],segEx[j],segEy[j],&intersectX,&intersectY)) {

        if ((intersectX!=segSx[i] || intersectY!=segSy[i])

        &&  (intersectX!=segEx[i] || intersectY!=segEy[i])) {

          if (segs==MAX_SEGS) return NO;

          segSx[segs]=segSx[i]  ; segSy[segs  ]=segSy[i]  ;

          segEx[segs]=intersectX; segEy[segs++]=intersectY;

          segSx[i   ]=intersectX; segSy[i    
]=intersectY; }

        if ((intersectX!=segSx[j] || intersectY!=segSy[j])

        &&  (intersectX!=segEx[j] || intersectY!=segEy[j])) {

          if (segs==MAX_SEGS) return NO;

          segSx[segs]=segSx[j]  ; segSy[segs  ]=segSy[j]  ;

          segEx[segs]=intersectX; segEy[segs++]=intersectY;

          segSx[j   ]=intersectX; segSy[j    
]=intersectY; }}}}




  //  Calculate the angle of each segment.

  for (i=0; i<segs; i++) segAngle[i]=angleOf(segEx[i]-segSx[i],segEy[i]-segSy[i]);




  //  4.  Build the perimeter polygon.

  c=startX; d=startY; a=c-1.; b=d; newX[0]=c; newY[0]=d; *corners=1;

  while (YES) {

    bestAngleDif=CIRCLE_RADIANS;

    for (i=0; i<segs; i++) {

      if (segSx[i]==c && segSy[i]==d && (segEx[i]!=a || segEy[i]!=b)) {

        angleDif=lastAngle-segAngle[i];

        while (angleDif>=CIRCLE_RADIANS) angleDif-=CIRCLE_RADIANS;

        while (angleDif< 0             ) angleDif+=CIRCLE_RADIANS;

        if (angleDif<bestAngleDif) {

          bestAngleDif=angleDif; e=segEx[i]; f=segEy[i]; }}

      if (segEx[i]==c && segEy[i]==d && (segSx[i]!=a || segSy[i]!=b)) {

        angleDif=lastAngle-segAngle[i]+.5*CIRCLE_RADIANS;

        while (angleDif>=CIRCLE_RADIANS) angleDif-=CIRCLE_RADIANS;

        while (angleDif< 0             ) angleDif+=CIRCLE_RADIANS;

        if (angleDif<bestAngleDif) {

          bestAngleDif=angleDif; e=segSx[i]; f=segSy[i]; }}}

    if ((*corners)>1 && c==newX[0] && d==newY[0] && e==newX[1] && f==newY[1]) {

      (*corners)--; return YES; }

    if (bestAngleDif==CIRCLE_RADIANS || (*corners)==MAX_SEGS) return NO;

    newX[ *corners   ]=e; lastAngle-=bestAngleDif+.5*CIRCLE_RADIANS;

    newY[(*corners)++]=f; a=c; b=d; c=e; d=f; }}

Special thanks to Moritz Ringler for making critical corrections to this code.

Sample Polygons

Here are three randomly-generated, sixteen-sided polygons with their perimeters traced in green by using the above code. In the third example, the “twist” does not cause the perimeter polygon to go counterclockwise — instead, it traces the area clockwise as illustrated by the red arrows.

Special Cases

Note that this technique may fail in special cases where the polygon has overlapping, colinear sides. This can be prevented by screening the polygon for defectiveness before calling polygonPerimeter().

Send me an e-mail!

Does the brace style in the above code sample freak you out? Click here to see it explained in a new window.

Back to tutorials.