Figure 1
©2007 Darel Rex Finley. This complete article, unmodified, may be freely distributed for educational purposes.
As of 2007-12-07, Wikipedia’s article on refraction contains no clear explanation of why refraction happens, and why a refraction should occur at a particular angle. The article does contain a section titled “Explanation,” but read that section from start to finish and you find nothing but re-statements of the fact of refraction.
In other articles (and discussions I have heard over the years), the issue of refraction is tied up with the idea that light “must” travel the fastest possible path, and refraction mysteriously provides that path. Why would it do that?
Here’s my best attempt to clearly answer both questions.

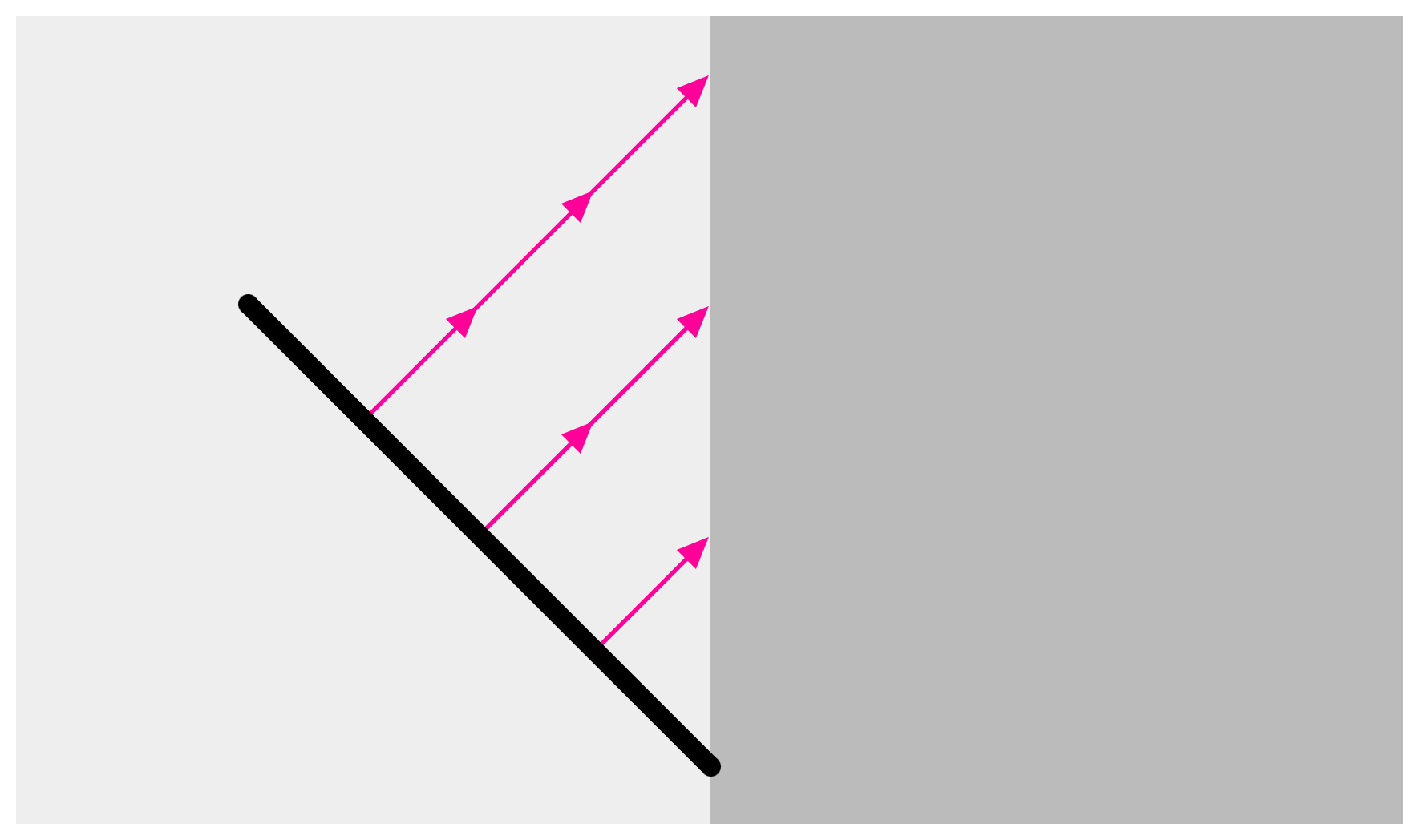
In Figure 1, we see a parallel wave (heavy black line) moving through a wave propagation medium (light grey area). The wave is passing into a another wave propagation medium (dark grey) that propagates waves at a different speed.
Each magenta arrow represents the distance the wave travels in one second. The triple magenta arrow illustrates that the part of the wave from which the triple arrow starts will strike the dark-grey medium three seconds from now. The double magenta arrow illustrates that the part of the wave from which it starts will strike the dark-grey medium two seconds from now. And the single magenta arrow illustrates that the part of the wave from which it starts will strike the dark-grey medium one second from now.
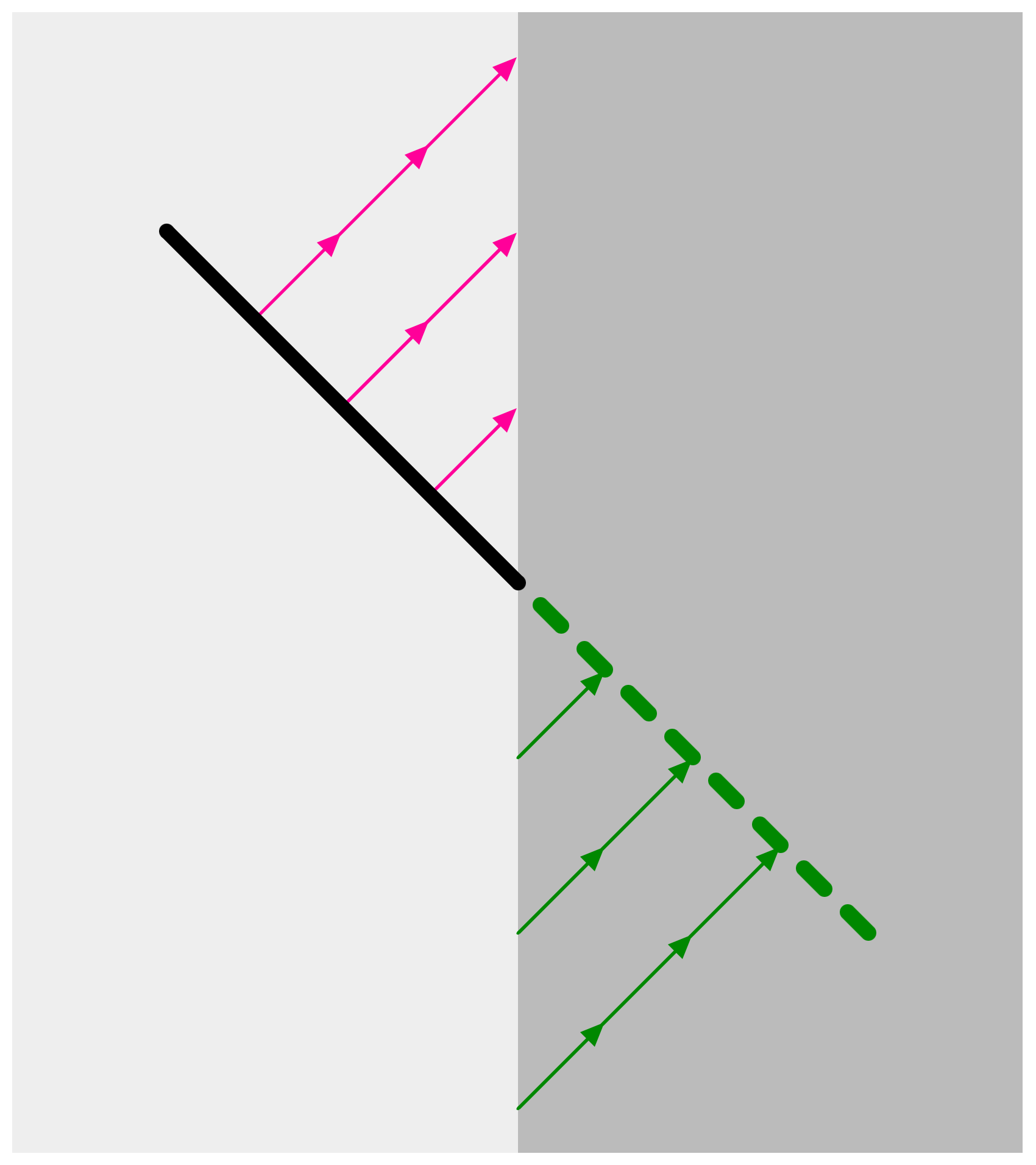
If the dark-grey medium afforded the same propagation speed as the light-grey medium, the wavefront would continue unchanged, as represented in Figure 2 by the heavy, green, dashed line. The green arrows show where the wave entered the dark-grey medium one second ago (single green arrow), two seconds ago (double green arrow), and three seconds ago (triple green arrow).
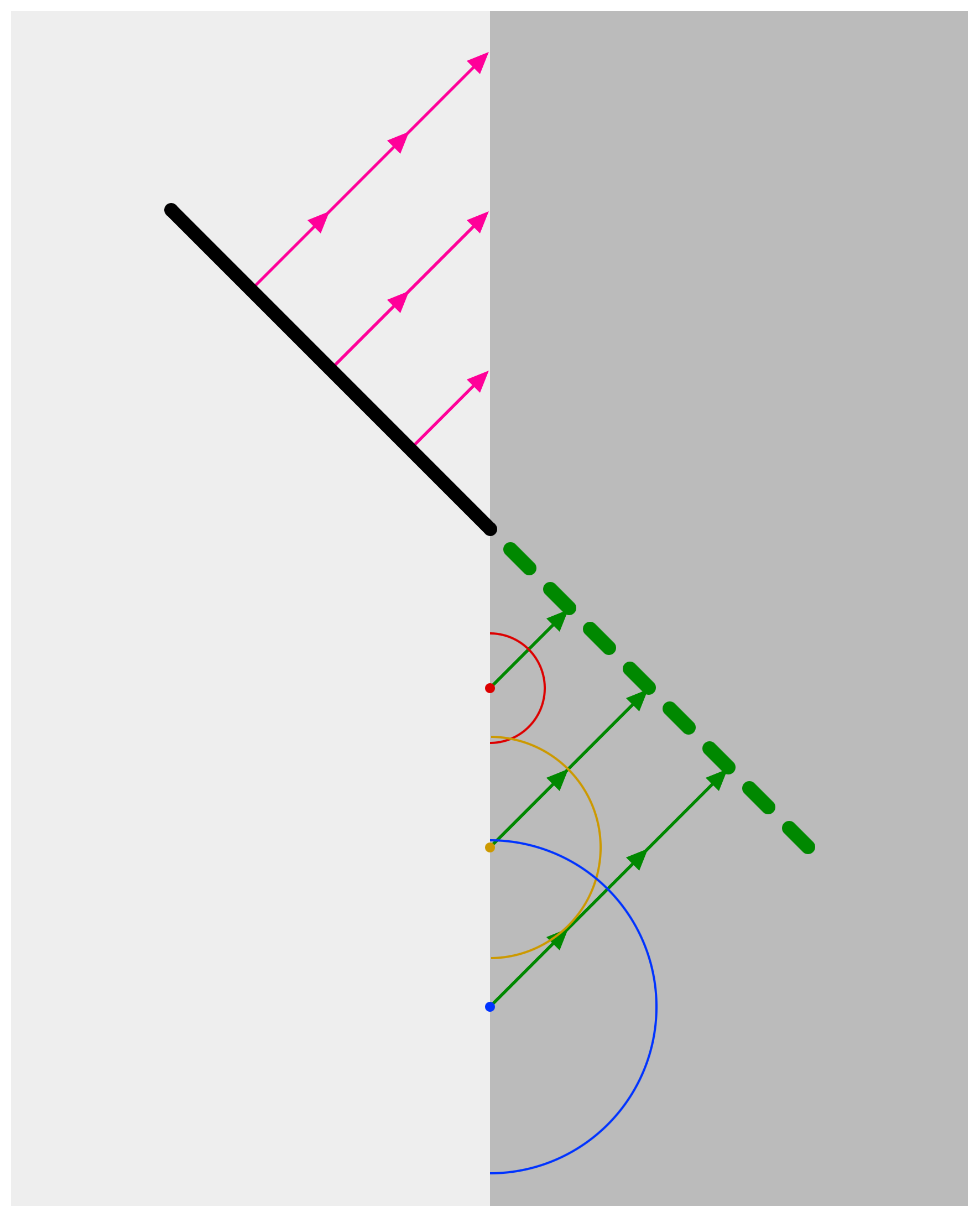
Suppose, however, that the dark-grey medium allows propagation at exactly half the speed of the light-grey medium. What happened to the wave as it entered the dark-grey medium? We don’t really know, so what we will do (see Figure 3) is draw three circles that represent the distance the new wave has travelled from each point. The red circle is all the points that are half of a green-arrow’s distance from the red entry point. The yellow circle is all the points that are half a double-green-arrow’s distance from the yellow entry point. And the blue circle is all the points that are half a triple-green-arrow’s distance from the blue entry point.
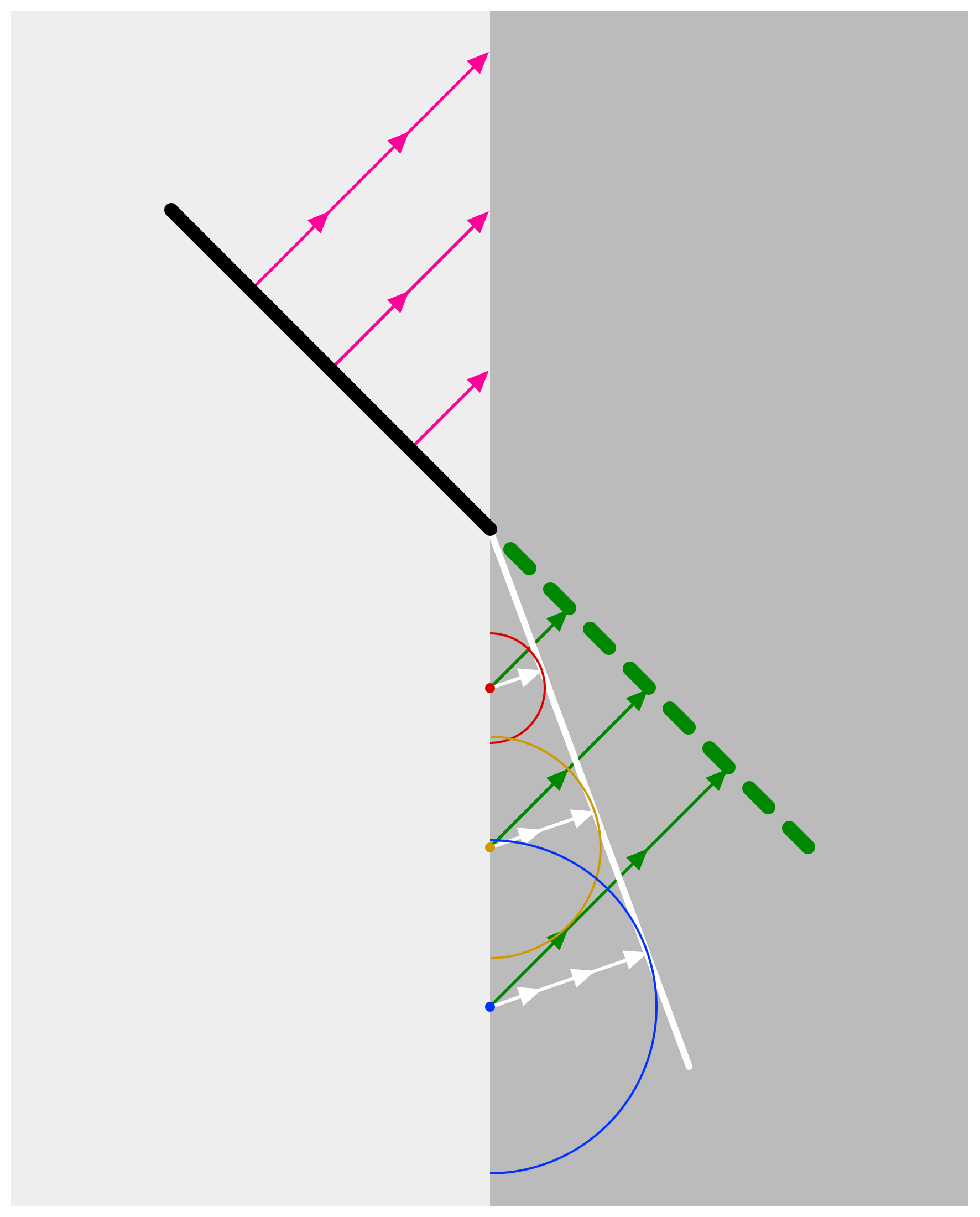
Now it is a simple matter (see Figure 4) to draw a tangent along the circles, and we can see what happened to the wave. It is now travelling in the direction of the white arrows, at half the speed it was travelling in the light-grey medium. The tangent (white line) is the new wavefront.
That’s it! That’s what causes refraction, and that’s what determines the angle of refraction. And it applies to any wave: sound waves, water waves, light waves.
Now — why would the angle of refraction happen to be the ideal angle for light to reach any point in the smallest possible time? One way to answer that question is that it’s just an interesting coincidence — since we already know what determines the angle of refraction (as described above), who cares if it happens to cause light to refract at the right angle to get to any particular target in the smallest possible time?
That the angle of refraction gets light to any target in the smallest possible time seems to be some sort of spooky property of light, in the same category as relativity or quantum mechanics. Does the light somehow know where it’s going? (Read up on “Fermat’s Principle” for more about that idea.) Or does the observation of the light at the receiver somehow affect its total course from initiator to receiver? No. The angle of refraction is the same for all waves, including waves as utterly unspooky as air-compression (sound) waves.
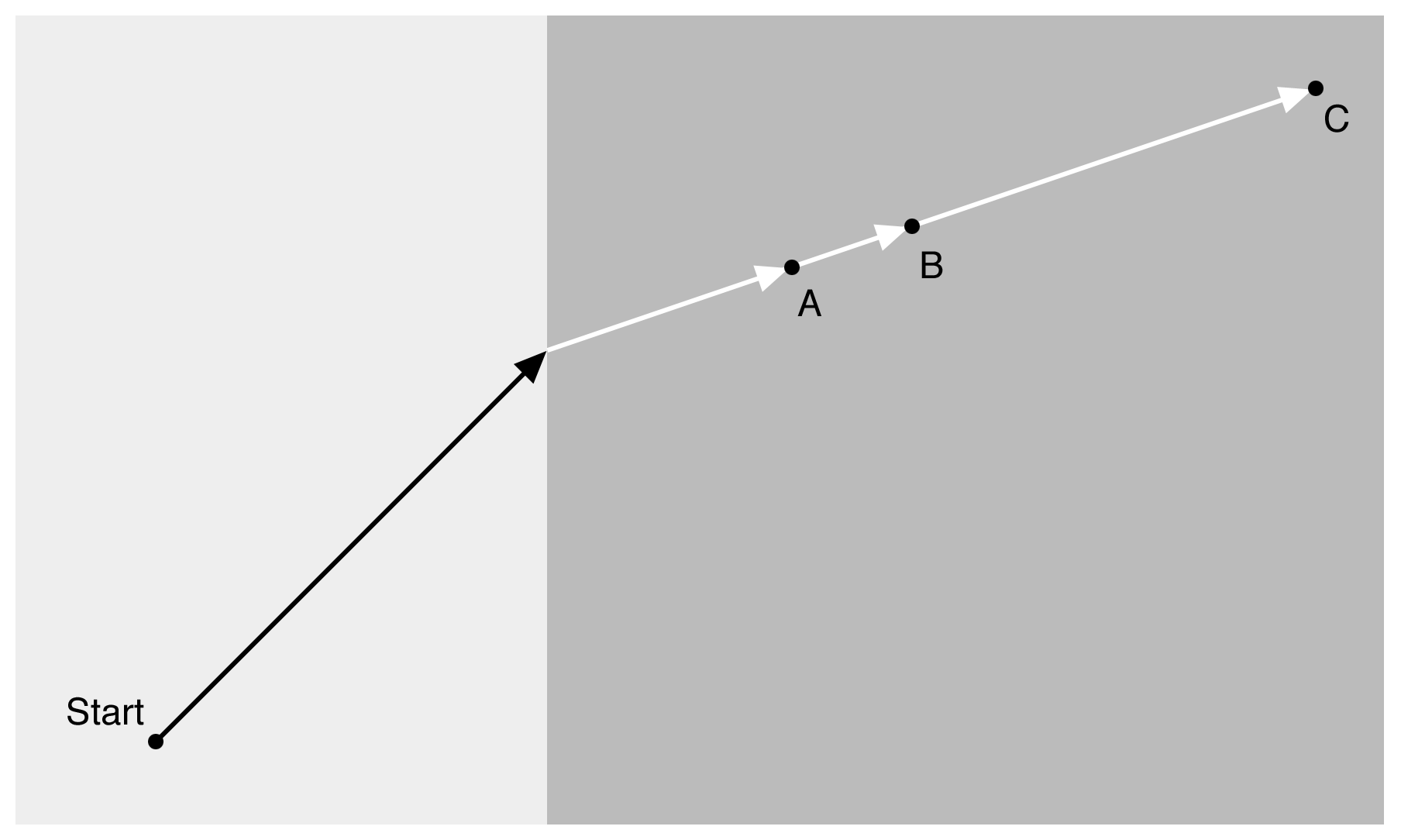
In Figure 5, the quickest path to any of the three targets, A, B, or C, involves the same entry point into the slower medium, with the same angle of refraction. The light has no idea where it’s going; it just happens that the refraction caused by the slower medium will get it to any target along the new trajectory in the smallest possible time.

Look at the crazy, multispeed, wave propagation medium in Figure 6. If a circular wave is started at point X, will it reach point Y in the smallest possible time? Yes, it will, as a matter of logical necessity. The “particles” of medium right next to X influence the particles next to them as quickly as they can, then those ones influence the ones next to them as quickly as they can, etc. The wave might reach Y by more than one path, but the fastest path will get there first, by definition — that’s what fastest means.
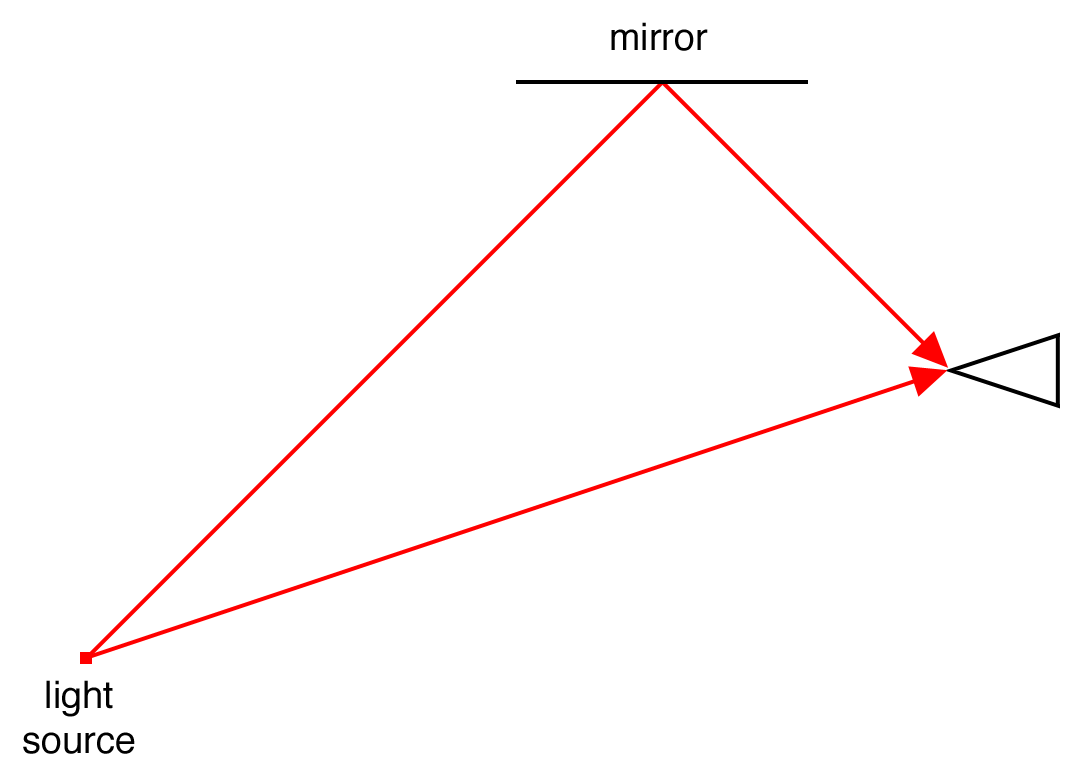
Here’s a simpler way to demonstrate the same thing (Figure 7). Which path will light take from the light source to get to the tip of the triangle? Answer: Both. The direct path is quicker, and it will get there first. But the longer path (off the mirror) will also get there.
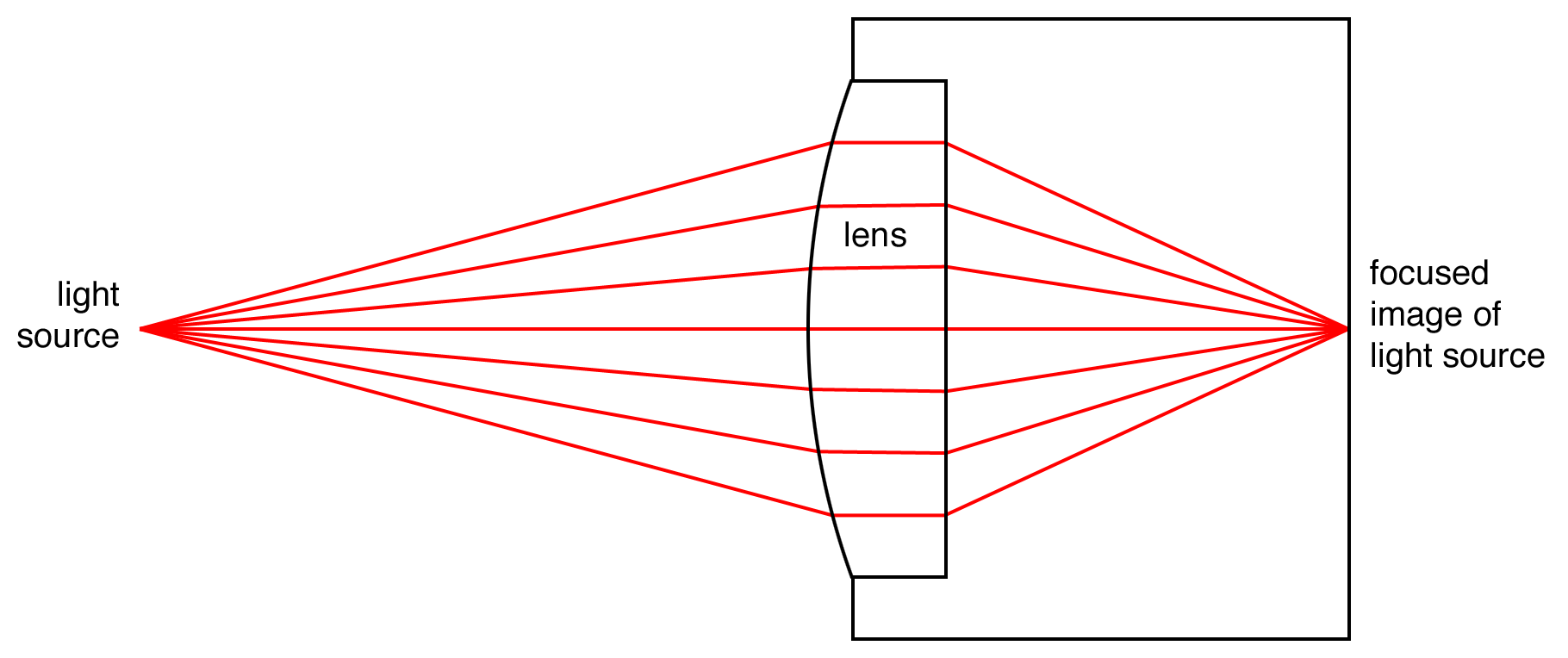
On the internet I found a New Mexico Tech refraction webpage that has a diagram like the one in Figure 8. It shows the lens of a camera redirecting multiple light rays from a point light source to a single point on the image receiver at the back of the camera. Which of these paths is the fastest? If you do the math, you find that they all take the same time — because the longer paths go through the light-slowing lens for a shorter distance. Oooh, is that because light “must” take the fastest path, and so it can take all those paths since they are all fastest?
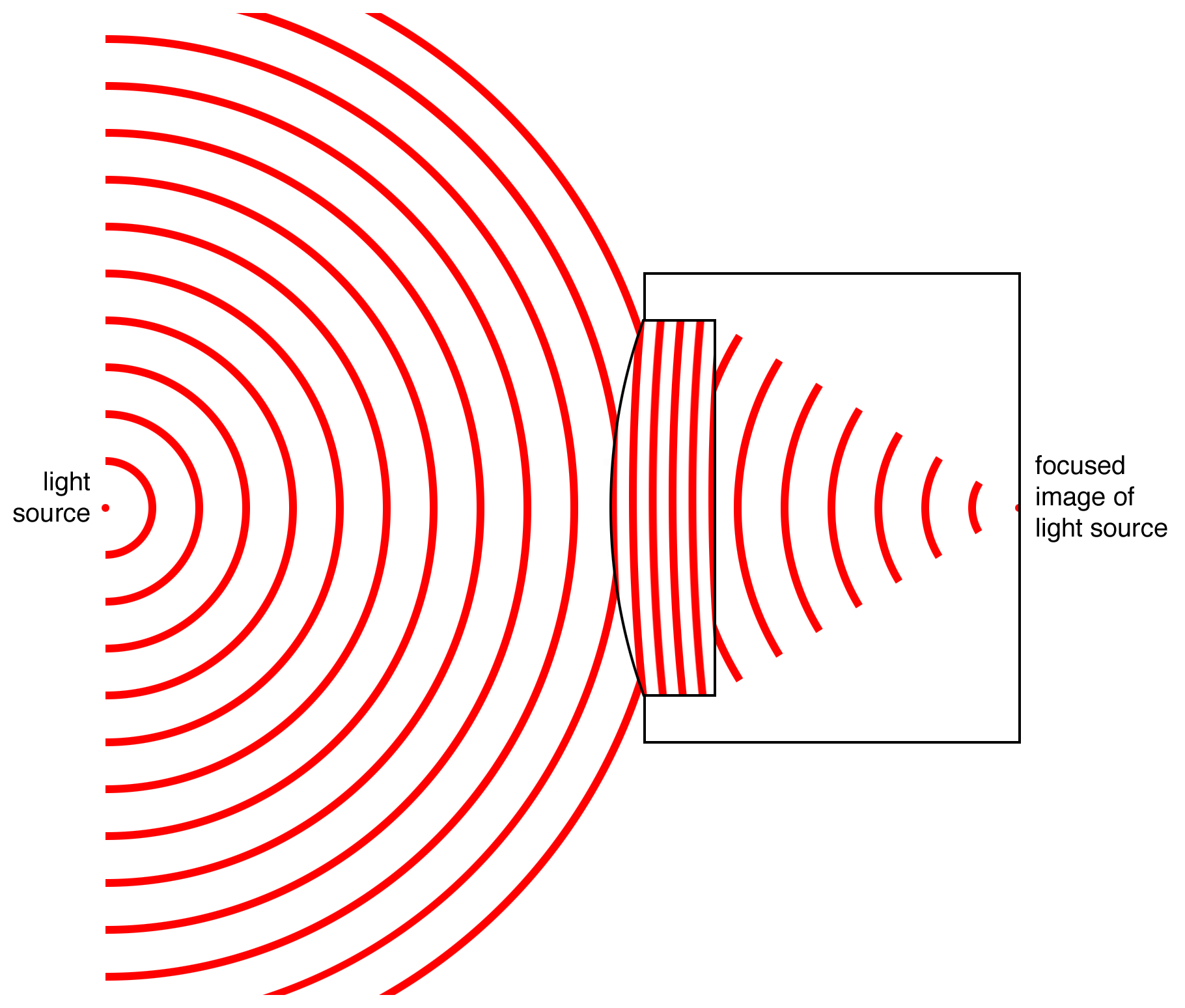
No, not really. Draw the same diagram (Figure 9) with waves and it’s not so impressive. Any 3-D wave that comes from, or collapses to, a point, must be spherical in shape. The only way a lens can make the wave condense to a point at the back of the camera is by shaping the wave into a semi-spherical configuration. As the wave condenses to a point, it of course arrives at that point at the “same time.”
That same webpage also shows a picture like Figure 10, which illustrates light emanating from the center of an oval. The oval is a mirror, and the light reflects back to the source from four different points on the surface of the mirror. According to the page, this shows that light can take the shortest or longest path. Say what? So much for light always taking the fastest path. And isn’t the shortest path from a light source back to that same light source just zero? — i.e. to already be there right when the light is emitted? And isn’t the longest path simply to never come back?

Figure 11 shows a different setup of my own design. Light from a light source goes out to five different mirrors at five different distances, and arrives back at the source at five different times. Clearly, no rule about the fastest or longest path applies at all.
Send me an e-mail!
Back to Tutorials.