Calculus Without Calculus — Solving Geometric Calculus Problems With Simple Vector Geometry
© Copyright 2005 Darel Rex Finley. All rights reserved. This article, with illustrations and copyright notice intact, may be freely distributed for educational purposes.
September, 2005



Most (if not all) geometric calculus problems can be solved using simple vector geometry, with no calculus derivatives. Perhaps these problems are useful for teaching the general principles of calculus, but they create the false impression that calculus is needed to solve them, and students are generally not told that the problems can be easily solved without calculus.

Let’s examine four calculus problems from a nice website created by Dr. Abdelkader Dendane, and see how they can be solved with simple geometry:


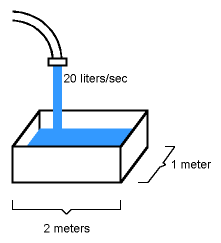
1. A rectangular, 1-meter-by-2-meter water tank is being filled at 20 liters/sec. How fast is the water level rising?



(This example doesn’t exactly use vectors, but is still relevant to the discussion.)

The area of the water’s surface is  100 cm * 200 cm  =  20,000 sq. cm.

A liter is 1,000 cu. cm, so  20 liters/sec  =  20,000 cu. cm/sec.

   (20,000 cu. cm/sec) / (20,000 sq. cm)  =  1 cm/sec.

That problem was easy because everything’s changing at nice, constant rates. But even if they aren’t, the same methods still work. Suppose we have a conical tank, a spherical tank, or whatever, and it is being filled at 20 liters/sec. If the current surface area of the water is 20,000 sq. cm, then the water is currently rising at 1 cm/sec. That’s all there is to it!

This technique also works for expanding-balloon (sphere) problems. Just use this simple formula:

   current surface area  *  current radial change-rate  =  current volume change-rate

Example: A sphere has a radius of 100 ft. The radius is currently changing at a rate of -1 ft/sec. This radius change-rate is accelerating by -8 ft/sec/sec. When the sphere hits zero volume, at what rate is its volume changing?

Answer: current surface area (zero) * current radial change-rate (who cares)  =  current volume change-rate (zero). The answer is 0. Do the calculus and you’ll get the same result.


2. You’re on the ground, watching an airplane fly away from you at 500 km/hr (.1389 km/sec), at a fixed altitude of 5 km. Currently, you observe the plane to be at 25° up from the ground. At what rate is this angle changing?



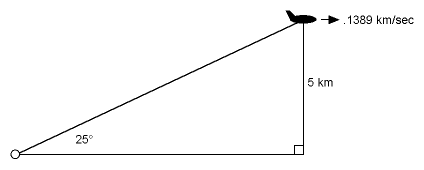
This looks tricky because as the plane gets farther and farther away, the angle diminishes more and more slowly. But actually, that’s irrelevant. The problem only wants to know how fast the angle is diminishing now, not at some time in the future or past. So let’s draw in some simple velocity vectors, and use a little trig to find the dimensions of the lines we need:



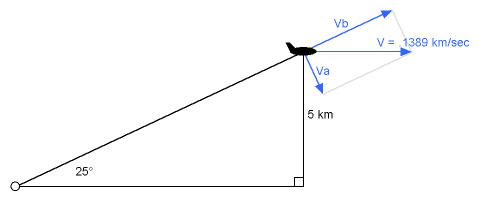
The blue vectors do not represent distances, but rather velocities. The plane’s velocity V can be broken into two component vectors Va and Vb. Va represents the plane’s motion across your field of vision, and Vb represents the plane’s motion away from you. Now it’s a simple matter to divide Va by your distance from the plane to get radians:

   Va  =  .1389 km/sec * sin(25°)  =  .05870 km/sec

   distance  =  5 km / sin(25°)  =  11.83 km

   Va / distance  =  (.05870 km/sec) / (11.83 km)  =  .004962 radians/sec

Now convert to degrees, and you get the same answer the website derived via calculus:

   (.004962 radians/sec) * (57.30°/radian)  =  .2843°/sec  ~=  .3°/sec

Don’t forget to make your answer negative, to signify that the angle is decreasing, not increasing.


3. You are standing in a straight road, but need to get to a location in a field by the side of the road. The target location is 10 km down the road from you, and 5 km from the road. You can move 5 km/hr on the road, but only 3 km/hr in the field. Assuming you want to get to your target as quickly as possible, how far you should you travel on the road before exiting the road and cutting through the field, straight to your target?



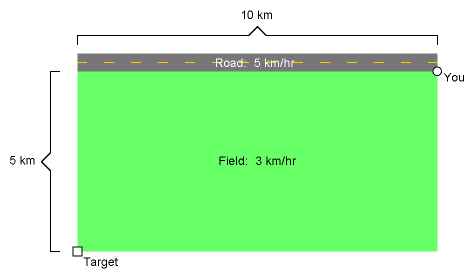
Can this problem be solved with vector geometry? It sure can. First, look at this diagram, which shows the plan of immediately exiting the road and walking diagonally through the field to the target:



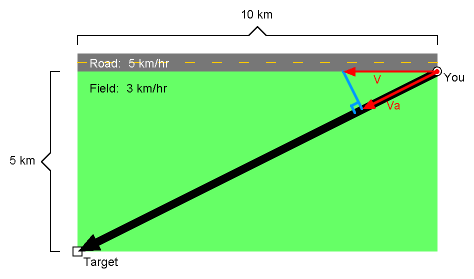
The red vector V illustrates an arbitrarily small move of the exit point down the road. Vector Va is the degree to which the field portion of the trip will be decreased by such a move. V is detrimental to your time, but Va is beneficial. Which is worth more, Va or V? (Keep in mind that the detriment of V must be multiplied by 3/5 when comparing with the benefit of Va, since you can only travel 3/5 as fast in the field.) It is obvious (or can be seen with a little quick math) that Va is greater than V * 3/5. So exiting the road immediately is not the best strategy.

Now, perform the same analysis on the plan of traveling 10 km down the road before exiting:



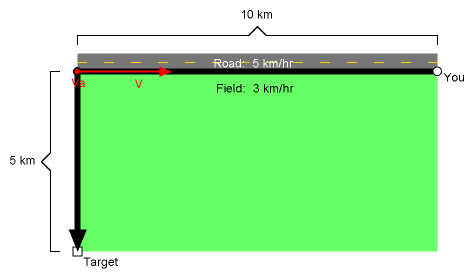
Vector V represents a reduction of the road portion by exiting sooner than 10 km, and vector Va represents the detriment of having to travel farther through the field. Va is not even visible because its magnitude is zero! So the 10 km strategy is also suboptimal.

That means that the optimal exit point must be somewhere in the middle of the 10km stretch of road. But where? Here’s how we find out:



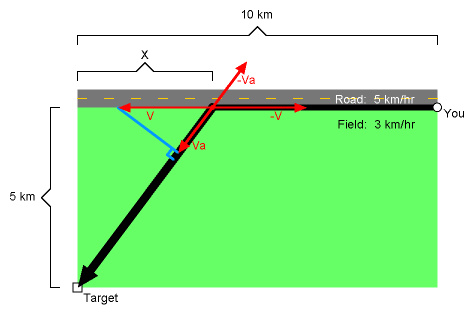
In this diagram, the detriment of V is exactly counterbalanced by the benefit of Va (keeping in mind that V must be multiplied by 3/5 when comparing to Va). And, by the same token, the benefit of -V (times 3/5) is exactly counterbalanced by the detriment of -Va. So nothing is to be gained by moving the exit point in either direction along the road. This is our optimal exit point.

Note that the right triangle with sides X (a leg) and 5 km (a leg) and the right triangle with sides V (hypotenuse) and Va (a leg) share one of their non-right angles — that means the two triangles must be proportionate to each other. That proportionality and the Pythagorean theorum give us the formula:

   Va / V  =  X / sqrt(X*X + 5km*5km)

Knowing that Va / V is three fifths, we can proceed with:

   3/5  =  X / sqrt(X*X + 25 sq. km)

   9/25  =  X*X / (X*X + 25 sq. km)

   (9/25) (X*X + 25 sq. km)  =  X*X

   (9/25) X*X + 9 sq. km  =  X*X

   9 sq. km  =  X*X - (9/25) X*X

   9 sq. km  =  (1 - 9/25) X*X

   9 sq. km  =  (16/25) X*X

   3 km  =  (4/5) X

   (15/4) km  =  X

   X  =  3.75 km

Therefore, you should exit the road after traveling 10 km minus 3.75 km, which is 6.25 km. (Dendane’s site is “rounded” to 6.26 km; I’m not sure why. The answer is exactly 6.25 km.)


4. You have 400 meters of fence with which to build a hog pen, and you are required to make your pen square or rectangular. You want the largest possible area within the pen — what should its dimensions be?



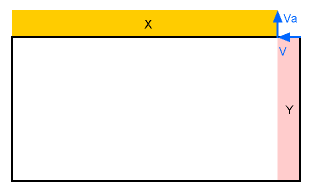
In the above diagram, vector V represents an arbitrarily small reduction of the long side of the pen, and Va represents the corresponding increase of the short side of the pen. You can see that the area gained (X) has to be larger than the area lost (Y), because rectangles X and Y both have one identically lengthed side, but the other side is longer for X. Therefore, making the pen more square will always increase its area. So the maximum achievable area has to be a perfect square. Your pen should be 100 meters on each side.


That’s all for now. If you know of any other geometric calculus problems that might need to be addressed here, please send me an e-mail.


Quicksort | Point-in-polygon | Mouseover menus | Gyroscope | Osmosis | Polarizer experiment | Calculus without calculus | Overlapping maze