|
|
Ultra-Easy Polygon Area Algorithm With C Code Sample
©2006 Darel Rex Finley. This complete article, unmodified, may be freely
distributed for educational purposes.
So you googled the internet for area-of-polygon algorithms and found only cryptic, greek formulas, or pages telling you to
break your polygon up into lots of little triangles? Did it make you want to retch violently and shoot
yourself? Ahh...sweet relief...here’s the Frappuccino of which you seek:
// Public-domain function by Darel Rex Finley, 2006.
double polygonArea(double *X, double *Y, int points) {
double area=0. ;
int i, j=0 ;
for (i=0; i<points; i++) {
j++; if (j==points) j=0;
area+=(X[i]+X[j])*(Y[i]-Y[j]); }
return area*.5; }
|
[Whoa! Since I wrote this page (earlier today), I found that Paul
Bourke’s pages include a C function
very similar to mine. Even some of the variable names are eerily identical! I swear I didn’t copy it
— he and I must be from the same generation of programmers.]
That’s all there is to it! Better than rejuvenation.
This function expects your polygon to be traced clockwise — if it’s traced counterclockwise, the
function still works but returns a negative value for the area.
|
|
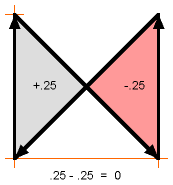
If your polygon crosses itself (i.e. is not “simple” in geometry lingo) then the parts of
the polygon that are traced clockwise count as positive area, and the parts that are traced counterclockwise count as
negative area. For example, the following, self-crossing polygon has zero area: 1,0,
1,1, 0,0, 0,1
(If you want to calculate the area of the polygon without running into problems like negative area, and overlapping areas
described below, you should use the polygon perimeter
technique.)
|
|
|
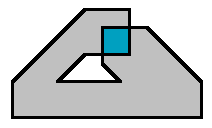A polygon can be self-crossing, yet still traced entirely clockwise. In that case, the area is
all positive, but the overlap area (blue) counts twice. In this example, the area returned would be:
grey + 2*blue A triple-overlap would result in tripling of the overlap area, etc.
|
|
|
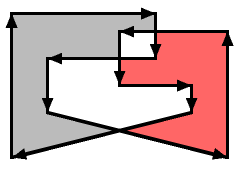If the polygon has a “twist,” such that part of the polygon has positive area and part
has negative area, and those two areas overlap, then the overlap area cancels out and does not count toward the total
area at all — because positive area plus negative area equals no area. In this example, the function
returns: grey - red
|
|
|
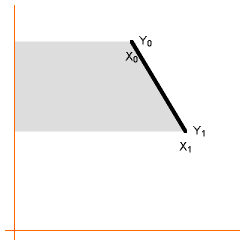So how does it work? Consider one side of the polygon. The formula is based on taking the
area to the left of the side, all the way to the Y-axis. That area is shaded grey in this
illustration.
|
|
|
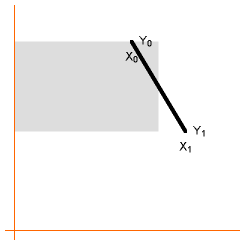That area is equal to the area of the grey rectangle in this picture. (You can make the area a
rectangle by removing a triangular grey piece from the bottom-right and putting it at the top-right.) So, the grey
area is easily calculated as (X0 + X1) / 2 (the rectangle’s width) * (Y0 -
Y1) (the rectangle’s height). This area is what we are adding to the accumulation variable
area each time through the loop — but the /2 is moved to the end of the function for purposes of
speed.
|
|
|
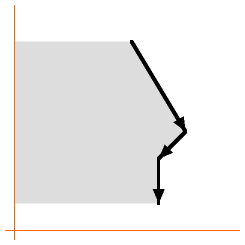Going down one side of the polygon adds all the grey area shown here.
|
|
|
Then going up the other side of the polygon substracts all the yellow area shown here,
because when a side is going up, Y0-Y1 is a negative number. The area that wasn’t
subtracted (grey) is the area of the polygon! That’s how it works. And you don’t have to start at
the top of the polygon — you can start anywhere, go all the way around, and the numbers will still add up to the same
value. (And, contrary to what you may have read on other sites, it doesn’t matter whether some or all of the
polygon’s corners are in the negative-X space, negative-Y space, or both — the result is still the same.
Try it!)
|
|
|
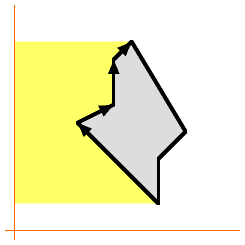
But what if the polygon is something messy like this? How do we know that it still
works?
|
|
|
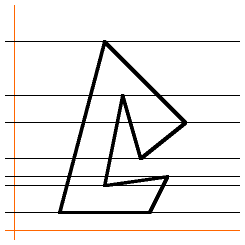Draw a horizontal line through every corner of the polygon. This divides the polygon into
horizontal strips which are partitioned by straight pieces of the polgyon’s sides.
|
|
|
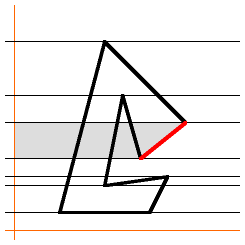Now look at just one strip. The right-most segment (red) adds the grey area to the
total...
|
|
|
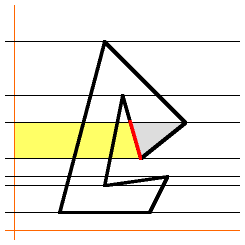...then the next segment removes the yellow area...
|
|
|
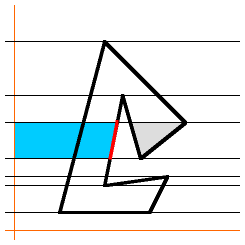...then the next segment adds the blue area...
|
|
|
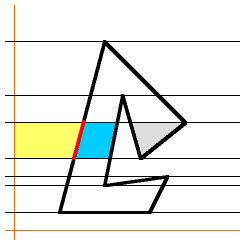...then the next segment removes the yellow area.
|
|
|
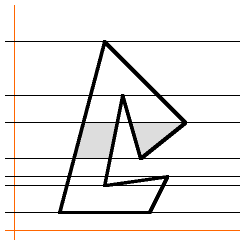Only the grey area (in this illustration) remains in the total, and it’s clearly the
polygon’s area (within this strip).
|
Now of course, our polygonArea() function is not breaking the polygon into strips like this. But since the
area to the left of any one side must be equal to the sum of that side’s strip-by-strip pieces, the grand total must
be the same, and must be equal to the area of the whole polygon.
Send me an e-mail!
|
Does the brace style in the above code samples
freak you out? Click here to see it explained in a
new window. |
|