// public-domain code by Darel Rex Finley, 2007
int nodes, nodeX[MAX_POLY_CORNERS], pixelX, pixelY, i, j, swap ;
// Loop through the rows of the image.
for (pixelY=IMAGE_TOP; pixelY<IMAGE_BOT; pixelY++) {
// Build a list of nodes.
nodes=0; j=polyCorners-1;
for (i=0; i<polyCorners; i++) {
if (polyY[i]<(double) pixelY && polyY[j]>=(double) pixelY
|| polyY[j]<(double) pixelY && polyY[i]>=(double) pixelY) {
nodeX[nodes++]=(int) (polyX[i]+(pixelY-polyY[i])/(polyY[j]-polyY[i])
*(polyX[j]-polyX[i])); }
j=i; }
// Sort the nodes, via a simple “Bubble” sort.
i=0;
while (i<nodes-1) {
if (nodeX[i]>nodeX[i+1]) {
swap=nodeX[i]; nodeX[i]=nodeX[i+1]; nodeX[i+1]=swap; if (i) i--; }
else {
i++; }}
// Fill the pixels between node pairs.
for (i=0; i<nodes; i+=2) {
if (nodeX[i ]>=IMAGE_RIGHT) break;
if (nodeX[i+1]> IMAGE_LEFT ) {
if (nodeX[i ]< IMAGE_LEFT ) nodeX[i ]=IMAGE_LEFT ;
if (nodeX[i+1]> IMAGE_RIGHT) nodeX[i+1]=IMAGE_RIGHT;
for (pixelX=nodeX[i]; pixelX<nodeX[i+1]; pixelX++) fillPixel(pixelX,pixelY); }}}
|
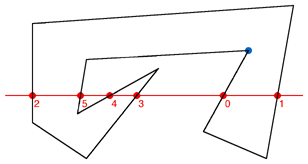 Figure 1
Figure 1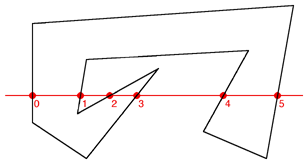 Figure 2
Figure 2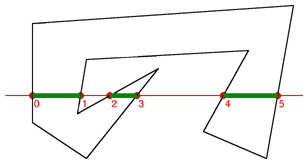 Figure 3
Figure 3