| |
Shortest Path Through A Concave Polygon With Holes
©2006 Darel Rex Finley. This complete article, unmodified, may be freely
distributed for educational purposes.
Inspired by Jonathan Walther’s RoBoat project.
The shortest path between two points inside a polygon may be a straight line:
Or, it may have to go around an obstacle:
Often, the shortest path will hug the wall of the polygon for part of its journey:
In fact, the shortest path will always consist of the startpoint and the endpoint, connected by a list of corners
from the polygon. (The above examples use 0, 1, and 4 corners of their polygons, respectively.)
If the polygon has “holes” — interior polygons of exclusion — then the shortest path may have to
dodge them:
 |
|
Note that in this example, the shortest path is not the simplest. The green line
represents a simpler way through the obstacles, but the blue path is shorter. |
How can we find the shortest path for any polygon (with or without holes) and any startpoint and endpoint? As
far as I know, an exhaustive search is required. However, the search can be optimized a bit so that it doesn’t
take as long as testing every possible path.
The technique used in the below code sample is to grow a spanning tree of points, starting at the
startpoint, where every point in the tree is connected back to the startpoint by the shortest possible path. When
this tree reaches the endpoint, the solution is found.
 |
|
Each tree-growing step adds not the closest connectible point, but rather the point that
can be connected back to the startpoint by the shortest possible total path. For example, the red point is closer
to the tree than the green point, but the green point gives a shorter total path back to the startpoint.
Adding nodes to the spanning tree in this manner ensures that every point is connected back to the startpoint by
the shortest possible path, and therefore that when we reach the endpoint, we will have reached it by the
shortest possible path. |
Code Sample
This code is C, but is based on structs that need to be defined. I have never compiled it, so if you discover a
bug, please do let me know!
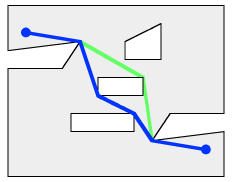
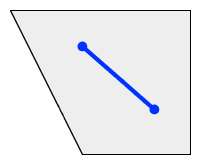
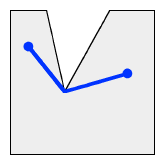
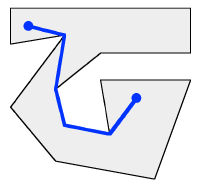
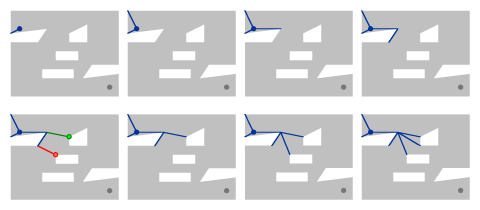
// Public-domain code by Darel Rex Finley,
2006.
// (This function automatically knows that
enclosed polygons are "no-go"
// areas.)
boolean pointInPolygonSet(double testX, double testY, polySet allPolys) {
bool oddNodes=NO ;
int polyI, i, j ;
for (polyI=0; polyI<allPolys.count; polyI++) {
for (i=0; i< allPolys.poly[polyI].corners; i++) {
j=i+1; if (j==allPolys.poly[polyI].corners) j=0;
if ( allPolys.poly[polyI].y[i]< testY
&& allPolys.poly[polyI].y[j]>=testY
|| allPolys.poly[polyI].y[j]< testY
&& allPolys.poly[polyI].y[i]>=testY) {
if ( allPolys.poly[polyI].x[i]+(testY-allPolys.poly[polyI].y[i])
/ (allPolys.poly[polyI].y[j]
-allPolys.poly[polyI].y[i])
* (allPolys.poly[polyI].x[j]
-allPolys.poly[polyI].x[i])<testX) {
oddNodes=!oddNodes; }}}}
return oddNodes; }
// This function should be called with the full set of *all* relevant polygons.
// (The algorithm automatically knows that enclosed polygons are “no-go”
// areas.)
//
// Note: As much as possible, this algorithm tries to return YES when the
// test line-segment is exactly on the border of the polygon,
particularly
// if the test line-segment *is* a side of a polygon.
bool lineInPolygonSet(
double testSX, double testSY, double testEX, double testEY, polySet allPolys) {
double theCos, theSin, dist, sX, sY, eX, eY, rotSX, rotSY, rotEX, rotEY, crossX ;
int i, j, polyI ;
testEX-=testSX;
testEY-=testSY; dist=sqrt(testEX*testEX+testEY*testEY);
theCos =testEX/ dist;
theSin =testEY/ dist;
for (polyI=0; polyI<allPolys.count; polyI++) {
for (i=0; i< allPolys.poly[polyI].corners; i++) {
j=i+1; if (j==allPolys.poly[polyI].corners) j=0;
sX=allPolys.poly[polyI].x[i]-testSX;
sY=allPolys.poly[polyI].y[i]-testSY;
eX=allPolys.poly[polyI].x[j]-testSX;
eY=allPolys.poly[polyI].y[j]-testSY;
if (sX==0. && sY==0. && eX==testEX && eY==testEY
|| eX==0. && eY==0. && sX==testEX && sY==testEY) {
return YES; }
rotSX=sX*theCos+sY*theSin;
rotSY=sY*theCos-sX*theSin;
rotEX=eX*theCos+eY*theSin;
rotEY=eY*theCos-eX*theSin;
if (rotSY<0. && rotEY>0.
|| rotEY<0. && rotSY>0.) {
crossX=rotSX+(rotEX-rotSX)*(0.-rotSY)/(rotEY-rotSY);
if (crossX>=0. && crossX<=dist) return NO; }
if ( rotSY==0. && rotEY==0.
&& (rotSX>=0. || rotEX>=0. )
&& (rotSX<=dist || rotEX<=dist)
&& (rotSX< 0. || rotEX< 0.
|| rotSX> dist || rotEX> dist)) {
return NO; }}}
return pointInPolygonSet(testSX+testEX/2.,testSY+testEY/2.,allPolys); }
double calcDist(double sX, double sY, double eX, double eY) {
eX-=sX; eY-=sY; return sqrt(eX*eX+eY*eY); }
void swapPoints(point *a, point *b) {
point swap=*a; *a=*b; *b=swap; }
// Finds the shortest path from sX,sY to eX,eY that stays within the polygon set.
//
// Note: To be safe, the solutionX and solutionY arrays should be large enough
// to accommodate all the corners of your polygon set (although it is
// unlikely that anywhere near that many elements will ever be
needed).
//
// Returns YES if the optimal solution was found, or NO if there is no solution.
// If a solution was found, solutionX and solutionY will contain the coordinates
// of the intermediate nodes of the path, in order. (The startpoint and endpoint
// are assumed, and will not be included in the solution.)
bool shortestPath(double sX, double sY, double eX, double eY, polySet allPolys,
double *solutionX, double *solutionY, int *solutionNodes) {
#define INF 9999999. // (larger than total
solution dist could ever be)
point pointList[1000] ; // (enough for all polycorners plus
two)
int pointCount ;
int treeCount, polyI, i, j, bestI, bestJ ;
double bestDist, newDist ;
// Fail if either the startpoint or endpoint is outside the polygon set.
if (!pointInPolygonSet(sX,sY,allPolys)
|| !pointInPolygonSet(eX,eY,allPolys)) {
return NO; }
// If there is a straight-line solution, return with it immediately.
if (lineInPolygonSet(sX,sY,eX,eY,allPolys)) {
(*solutionNodes)=0; return YES; }
// Build a point list that refers to the corners of the
// polygons, as well as to the startpoint and endpoint.
pointList[0].x=sX;
pointList[0].y=sY; pointCount=1;
for (polyI=0; polyI<allPolys.count; polyI++) {
for (i=0; i<allPolys.poly[polyI].corners; i++) {
pointList[pointCount].x=allPolys.poly[polyI].x[i];
pointList[pointCount].y=allPolys.poly[polyI].y[i]; pointCount++; }}
pointList[pointCount].x=eX;
pointList[pointCount].y=eY; pointCount++;
// Initialize the shortest-path tree to include just the startpoint.
treeCount=1; pointList[0].totalDist=0.;
// Iteratively grow the shortest-path tree until it reaches the endpoint
// -- or until it becomes unable to grow, in which case exit with failure.
bestJ=0;
while (bestJ<pointcount-1) {
bestDist=INF;
for (i=0; i<treeCount; i++) {
for (j=treeCount; j<pointCount; j++) {
if (lineInPolygonSet(
pointList[i].x,pointList[i].y,
pointList[j].x,pointList[j].y,allPolys)) {
newDist=pointList[i].totalDist+calcDist(
pointList[i].x,pointList[i].y,
pointList[j].x,pointList[j].y);
if (newDist<bestDist) {
bestDist=newDist; bestI=i; bestJ=j; }}}}
if (bestDist==INF) return NO; // (no solution)
pointList[bestJ].prev =bestI ;
pointList[bestJ].totalDist=bestDist;
swapPoints(&pointList[bestJ],&pointList[treeCount]); treeCount++; }
// Load the solution arrays.
(*solutionNodes)= -1; i=treeCount-1;
while (i> 0) {
i=pointList[i].prev; (*solutionNodes)++; }
j=(*solutionNodes)-1; i=treeCount-1;
while (j>=0) {
i=pointList[i].prev;
solutionX[j]=pointList[i].x;
solutionY[j]=pointList[i].y; j--; }
// Success.
return YES; }
|
Shortest Path Around Obstacles
What if you want to find the shortest path around (or through/inbetween) one or more polygon-shaped obstacles? You can use
the same method. Just include one extra polygon: a big rectangle (or any other shape) that surrounds all the other polygons
and the startpoint and endpoint. Then, the obstacles become “holes” in that polygon, and the
shortest-path-through-polygon method (described above) will find the solution.
To find the shortest path around these polygons... |
|
...put a rectangular polygon around the whole problem, and it becomes a shortest-path-through-polygon
problem as discussed earlier in this page. |
Send me an e-mail!
|
Does the brace style in the above code sample freak
you out? Click here to see it explained in a new
window. |
|