Collatz Conjecture Analysis (But No Proof; Sorry)

2012.01.06   prev     next

ALAS, I find I am unable to develop a proof of the Collatz Conjecture. But in my attempts to do so, I have come up with a few interesting ways of analyzing the problem, that perhaps are worth sharing.

Hailstone

A “Hailstone” sequence goes like this: Start with any positive integer, say, 52. If the number is even, divide it by 2, otherwise multiply it by 3 and add 1. Since 52 is even, we will divide it by 2, and get 26. Now, do the same thing again. Since 26 is even, we will divide it by 2 and get 13. Now, 13 is odd, so we will multiply it by 3 and add 1, resulting in 40.

Starting from 52, the hailstone sequence does this:

52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, etc.

Notice that the sequence settled into a three-number cycle: 1, 4, 2. This repeats forever.

Collatz Conjecture

The Collatz Conjecture says that no matter what positive integer you start with, your hailstone sequence will, in a finite number of steps, wind up repeating at 1, 4, 2. The challenge is to find a rigorous logical-mathematical proof that the conjecture is true.

Analysis

Let’s lay out the positive integers into a quadrant grid like so:

  19  38  76  152  304  608  1216
  17  34  68  136  272  544  1088
  15  30  60  120  240  480   960
  13  26  52  104  208  416   832
  11  22  44   88  176  352   704
   9  18  36   72  144  288   576
   7  14  28   56  112  224   448
   5  10  20   40   80  160   320
   3   6  12   24   48   96   192
   1   2   4    8   16   32    64

The left column is all the odd numbers (1, 3, 5, 7, etc.), and each row is a doubling sequence. Except for the left-most column, all the numbers are even, so at first glance, it appears that this arrangement contains mostly even numbers. But appearances are deceiving: The chart contains every positive integer, and contains each one exactly once. This is true because:

• All the odd numbers are in the left column, with no repeats.
• Since any even number can be converted to an odd number by dividing it by 2 one or more times, and all the odd numbers are included, then all the even numbers must be included.
• Since any one doubling sequence (row) does not include the same value twice, and each row starts with a unique odd number, no even number can be included more than once.

Therefore the layout contains each counting number exactly once.

Because each row is a doubling sequence, the hailstone step of dividing an even number by 2 is equivalent to moving one column to the left. Therefore, if you are currently on any even number (i.e. on any column to the right of the left-most column), you simply move straight to the left until you reach the left-most column.

Since the left-most column is composed of odd numbers, when you are on it, you must multiply by 3 and add 1. This takes you to an even number in another row — unless you are on the number 1 (the bottom row), in which case it takes you to the number 4 in the same row. We know that the bottom row is the only row whose odd number goes to the same row because each row consists of numbers of the following form:

  n  2n  4n  8n  16n  .  .

This sequence does not include 3n, whose value falls in-between 2n and 4n. 3n+1, however, can reach 4n — but only if n is 1. So only the bottom row can go to itself. All other rows go to a different row than themselves.

Now we can think of the hailstone sequence as dealing with only odd numbers. Each odd number represents a row, and each odd number jumps to another row (i.e. to another odd number). The only odd number that jumps to itself is 1. (If we start the hailstone sequence on an even number, we can simply pretend that we started on the odd number that begins that number’s row.)

So our example sequence that started on 52 can be simplified to:

  13, 5, 1, 1, 1, etc.

(The conjecture is not yet proven, because we have not eliminated the possibility that two or more odd numbers are connected in an infinite loop, nor the possibility that a hailstone sequence could grow without limit.)

Every third row consists of numbers that are divisible by 3 (i.e. the rows that start with 3, 9, 15, 21, etc.). These rows can be discarded as effectively not part of the problem, because the hailstone sequence jumps to a new row with the operation 3n+1, which can never be divisible by 3. Hence, the rows 3, 9, 15, 21, etc. can serve only as a starting row for a hailstone sequence, but are never visited again. So we can simply pretend that a hailstone sequence that started on an odd multiple of 3 actually started on the next value in that sequence.

So the problem can be reduced to showing that all odd numbers that are not divisible by 3 eventually settle on the value 1. Those values are:

  1,5,7,11,13,17,19,23,25,etc.

(This looks like a set of prime numbers, but it isn’t — note the presence of the number 25.)

When an odd number n is subjected to 3n+1, it projects onto all other rows via a curve that looks like this:

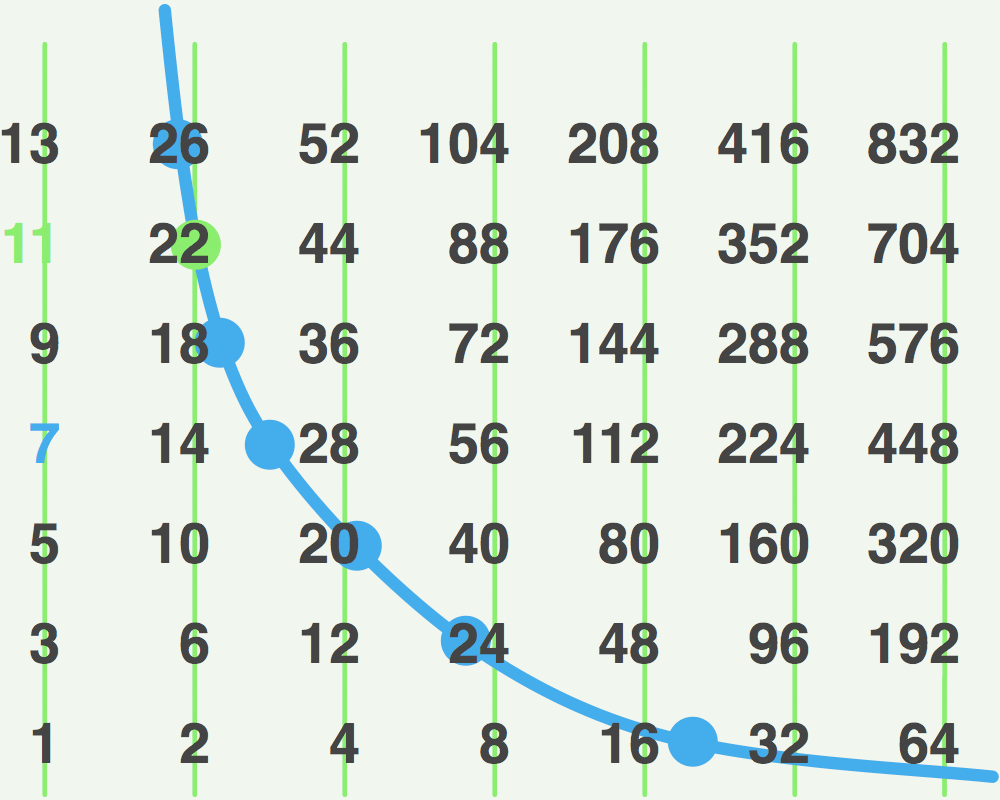
In this diagram, hailstone moves from the 7’s row to the 11’s row via 22.  11 is approximately 1.5 times 7.

This curve hits only one row at a column value, and it cannot hit at the left-most (odd) column since 3n+1 is always even. Therefore, if it hits a higher row, it must hit that row’s second column (the row’s first even column). Simple math indicates that the new n will be approximately 1.5 times the old n. So when (odds-only) hailstone goes up from its current row, it goes up to approximately 1.5 times the value of the old row. When it goes down, however, it can go down any distance at all, even jumping straight to the bottom row. Note: If it could be proven that any (odds-only) hailstone sequence cannot indefinitely maintain an average percentage value change greater than the average for all odd numbers, then that might constitute a proof of the conjecture.

Loops

The formula for an odd number n that returns to itself in, say, four (row-jumping) steps is:

     abc + 3ab + 3²a + 3³
 n = ————————————————————
          abcd - 3⁴

where a, b, c, and d are powers of 2 (not less than 2) that represent how much the number must be divided by to move it to the left-most column after landing in a new row.

The formula for an odd number n that returns to itself in five (row-jumping) steps is:

     abcd + 3abc + 3²ab + 3³a + 3⁴
 n = —————————————————————————————
               abcde - 3⁵

And so on.

If you set the values of all the power-of-2 variables (a, b, etc.) to 4, then the formula evaluates to 1, indicating that 1 is always a positive integer solution to the formula, and that it jumps to the value 4n (i.e. 4) with each row-jumping step.

For any of these formulas, if you could find any other combination of power-of-2 values that give an n value that is a positive integer other than 1, then (provided those power-of-2 values actually work with the hailstone rules), you would have disproven the conjecture by the discovery of an infinite loop that does not involve the bottom (n=1) row.

On the other hand, if you can prove that these formulas have no positive integer solution other than 1, then you have proven that there are no loops except at the bottom row.

It turns out to be fairly easy to show that if the power-of-2 variables are all at least 4, and any of them are greater than 4, then n evaluates to a number between 0 and 1. So the only cases we need to worry about are those in which one or more of the power-of-2 variables have the value 2. Playing around with these cases shows that n can be made negative (but we don’t care about that, only positive integers), and it can be made into positive values greater than 1, but they don’t appear to be integers. If there is some way to prove that they can’t be integers, then loops are eliminated except at the bottom row.

If There Are No Loops...

If you are able to prove that there are no loops except at 1, would it seal the conjecture? Maybe. You would still have to address the possibility that a hailstone sequence could become larger and larger without limit. There might be a way to show that that is impossible, that goes something like this:

Reverse hailstone is where you either multiply n by 2, or subtract 1 then divide by 3. The latter step, n′ = (n-1)/3, may be performed only if n is even and n-1 is divisible by 3, but the former step, n′ = 2n, may be performed on any value. So, reverse hailstone can be performed indefinitely (and it branches).

Reverse hailstone that starts on any row that is not the bottom row, cannot reach the bottom row, because if it could, then the bottom row would not be stuck in a forward-hailstone loop, and we know that it is.

If we already knew that a loop (other than at the bottom row) is not possible, then if forward hailstone starting at x grows without limit, then what does reverse hailstone starting from x do? To avoid a loop, it too must grow without limit — and not just by use of n′ = 2n — its row-jumping branches must grow without limit, otherwise the rows will become exhausted and a loop will be discovered. So there would have to be a hailstone sequence that comes down from infinity, then turns around and goes back up to infinity. My intuition tells me that this cannot be, but I have no formal proof.

Prime Factors

Another way to analyze Collatz is via the prime factorization of a number. Suppose you’re currently on a row that starts with n. n can be represented as a set of prime numbers multiplied together. We know that the numbers 2 and 3 won’t be among those primes, because n is odd and we’ve already eliminated divisible-by-3 rows from relevancy. So the prime factors will all be 5 or greater.

Now we move from n to another row, which starts with n′. Like n, n′ does not have 2 or 3 among its prime factors. Furthermore, it does not have any of the prime factors that belong to n. We know this because the +1 step gets rid of all of the prime factors of n. The steps to get from n to n′ are:

a. Multiply by 3: This step appends 3 to the prime factorization, but otherwise doesn’t change it.

b. Add 1: This step kills all the current prime factors (including the 3), because if a number is divisible by x, and you add 1, then it’s no longer divisible by x. One or more 2s appear in the prime factorization, because the number is now even. Other prime factors, not present before this step, may appear (or may not).

c. Divide by 2 until the number is odd: This simply removes all the 2s that appeared in the previous step.

So with each row-jumping step, the number changes from a prime factorization that included no 2s or 3s, to a new prime factorization that also doesn’t include 2s or 3s, nor does it include any prime factors from the old row.

True But Unprovable?

In reasearching the Collatz Conjecture, I have found some material that says that a more general set of problems has been shown to be unprovable; yet the specific (a­bove-discussed) Collatz Conjecture may yet be provable. I have also found some material suggesting that the Collatz Conjecture may one day be found to be true-but-unprovable.

Call me uneducated, but I find the whole concept of “true but unprovable” to be inherently contradictory. Yes, I can conceive that a conjecture such as Collatz’s might be true (i.e. there might be no exceptions to it) and yet there might be no logical/mathematical proof of that conjecture for us to find. However, if that is the case, then it seems only logical to state that we will never know it. If the Collatz (or any other) Conjecture is true but unprovable, then our knowledge of the Conjecture will always be that we don’t know for sure whether it’s true or not, and that we haven’t found any exceptions, nor any proof that there are no exceptions.

In other words, if you can show that conjecture C is true-but-unprovable, then you have shown that C is true, and therefore you have proven it. Which means it’s not unprovable.

Now, of course, we might one day discover a proof that the Collatz Conjecture can’t be proven. OK, I can imagine that. But in that case, we will never know whether there isn’t some exception to the conjecture lurking in the set of counting numbers. (Unless/until we find one.) This proof of unprovability won’t eliminate that possibility; it will just prove that we can’t prove there aren’t exceptions. Any claim that includes “the conjecture is true” is tantamount to a proof, and thus the conjecture loses un­prov­a­bil­i­ty.

Confused? Here’s some clarification. Suppose that the following propositions happen to be true:

• The Collatz Conjecture is true; i.e. there are no exceptions to it. All positive integers behave as it posits.
• There is no logical/mathematical proof that the Collatz Conjecture is true.
• There is a logical/mathematical proof of the Collatz Conjecture’s unprovability.

In that case:

• We will never find an exception to the Collatz Conjecture.
• We will never know for sure that there isn’t an exception to the Collatz Conjecture.
• We may possibly discover the proof that the Collatz Conjecture is unprovable.
• We will never know that the Collatz Conjecture is “true but unprovable” (even though it is) — we will always have to wonder if it is unprovable because it is false, and we just haven’t found an exception yet.

Now, suppose that we define “true but unprovable” more precisely, to mean “true, but unprovable via technique set X?” OK, that might make more sense. But if a person claims to have shown that the Collatz Conjecture is:

(a) true, and
(b) unprovable via technique set X

then I’m only dimly interested in claim (b), while very interested in claim (a). Who cares about technique set X? If you’ve convinced yourself that there are no exceptions to the Collatz Conjecture, then I’d really like to know the specifics of how you convinced yourself of that. Whether the truth of the conjecture can also be established by some more limited set of techniques “X” is a far less interesting topic.

That’s All, Folks

And that’s all I’ve been able to figure out about the Collatz Conjecture. Don’t know if any of it can be developed further into a proof. I hope it was interesting.

Update 2012.01.18 — “Prime Factors” section added

Update 2012.08.20 — “True But Unprovable?” section added

Update 2014.10.21 — This analysis is continued here.

prev     next