The Non-Euclidean Geometry That Wasn’t There

2008.02.07   prev     next

WHAT is geometry? Where does it come from?

For centuries, mathematicians struggled over this subject, and always had to conclude that geometry is based on a set of arbitrary assumptions. Change those assumptions a little, they later said, and you get a very different form of geometry, which they dubbed “non-Euclidean” geometry. Non-Euclidean geometry seems counter-intuitive, and is hard if not impossible to visualize in your head; however, it seems it must be possible, because no internal inconsistencies can be found in its rules.

But... what if so-called “Euclidean” geometry could be shown to spring directly from using mathematics to build a dynamic system? That might shake things up. It might even reveal “non-Euclidean” geometry to be something massively less than it appears.

BWAH-HA-HA-HA.. — oh, excuse me. Frog in my throat.

A Dynamic System

Let’s build a dynamic system, shall we? A sort of mini “world,” in which things can happen.

First, to be dynamic, our system must be capable of change. So we need some entities that can change over time, between two or more states. To keep things simple, let’s go with the smallest number of states: two. We’ll call these entities “bits,” and call their two states 0 and 1.

Now, you can’t make a very interesting dynamic system if each dynamic element can have only two states. So let’s create a group of bits, and call it a “variable.” We’ll use, say, 64 bits, in a definite order. That way, each variable can, at any moment in time, be in one of 2⁶⁴ different states (values). That’s a lot of different values. Much better than two.

The 2⁶⁴ different values (combinations of sixty-four 0s and/or 1s) don’t mean much unless we give them an order. So let’s arbitrarily define an order for the 2⁶⁴ different values. It doesn’t really matter what order we use, as long as there is a first value, then a next value, then another, and so on, finally ending with a last value. For any given value (other than the first and last values), we should be able to identify the value immediately preceding it and immediately following it.

It turns out that the binary counting system is most convenient for creating such an order. In this system, the first value is all zeros, the next value is all zeros and a one, the next value is all zeros and a one and a zero, etc. Like so:

..00000000
..00000001
..00000010
..00000011
..00000100
..00000101
and so on, up to all ones:
..11111111

And, in using the binary counting progression for our value order, we indirectly have created a system of numerical addition, subtraction, multiplication (which is just repeated addition or subtraction), and division (an approximated inverse of multiplication).

Now, let’s create a list of items, where each item has three variables. We’ll call these variables X, Y, and D. The values of X and Y will be static, but the value of D will be dynamic. We’ll make 2¹²⁸ items in our list, and give each item a unique combination of X and Y values. So all possible combinations of X and Y will be used exactly once, and the D values will (for now) be unspecified. Later, when our dynamic system is “running,” the D value of each list item will be capable of change, but the X and Y will not.

What we have created, in effect, is a two-dimensional matrix of cells, where each cell has a fixed X and Y coordinate, but also has a dynamic value D that can change over time. That might be diagrammed like so:

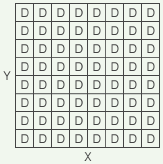
(simplified to 8x8 for illustration)

This is starting to look like a Cartesian coordinate system. And, in many ways, it already resembles one. But in other ways it doesn’t. For example, in the below diagram, what is the “distance” between the red cell and the blue cell?

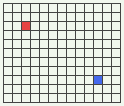
You could define it as the Pythagorean distance — i.e. sqrt(X_dif*X_dif + Y_dif*Y_dif), which in this case would be sqrt(8*8+6*6) = 10 — but that would be an arbitrary presumption of Euclidean geometric rules. In our dynamic system as so far described, there is no reason the “distance” between the red cell and blue cell couldn’t be defined as simply abs(X_dif) + abs(Y_dif), in this case 8+6 = 14. That might even make sense from the standpoint of the distance being the minimum number of single steps it takes to get from the red cell to the blue cell, where a single step is the smallest change possible to the X,Y coordinates of your location; i.e. to leave one coordinate unchanged, and move the other coordinate by just a single step up or down in the value order.

To establish the Pythagorean theorum at this point would surely lead to full-blown Euclidean geometry. But you can’t slap it in just because you measured some right triangles with a ruler in the real world, and they looked perfectly Pythagorean. We’re building a dynamic system from mathematic elements here, and the Pythagorean distance system doesn’t spring forth naturally from a two-dimensional array of dynamic data cells.

Does it?

We need some rules by which our dynamic values D can change over time; by which data can “move around” in our matrix. Let’s go for something really simple. How about this: With every frame (tick of the time clock), each cell will share some minority of its D value (say, 10% of it) with the cells that are most similar to itself in terms of X and Y — in other words, with the cells that are identical on one coordinate, and just one position away on the other coordinate. (This is the “smallest step” described above.) Each cell thus has four such “neighbor” cells, with which it shares 10% of its D value. It shares the 10% equally among its four neighbors, so that the sharing cell loses 10% of its D value, and each of its four neighbors receives one quarter of that 10% (i.e. 2.5%). So the total of all D values in the entire matrix never changes; it just moves around.

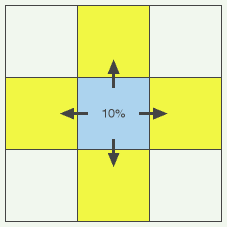
It’s pretty easy to predict what such a system will do. Local concentrations of D value will simply spread out until all the D value is smoothly distributed across the whole matrix. Nothing too spectacular here.

But how will it spread out? What will that look like? Let’s run a simulation and find out.

frame 0

In this image, all the cells in a 256-by-256 matrix have a D value of zero, except one cell in the approximate middle, which has a D value of ten million. That’s about the simplest starting condition we can come up with to see what happens to a local concentration of D. This pictorial representation caps out at 255 (white), but we need a really large starting value so we can see how the data expands outward.

Now let’s run our dynamic system for ten frames.

frame 10

Hmm, that’s interesting. It’s kind of circular, maybe. A little diamond-shaped? Hard to tell at this early stage. Let’s run it some more.

frame 50

Say, that looks kind of circular. Maybe a lot. Let’s run it some more.

frame 100

Ooo. That’s really circular.

frame 500

OK, that’s not just circular — that’s maybe the most perfectly circular thing I’ve ever drawn with a computer, even when I was running code that explicitly included the Pythagorian formula or used the OS’s sine and cosine functions! But this program includes no such formulas or functions.

frame 2000

Yup, very circular spread. Pretty much undeniable.

So the time it takes a significant quantity of D to reach a particular cell from another (reasonably distant) cell is governed by the Pythagorian distance, with no explicit coding of the Pythagorian formula; nothing but the simplest conceivable sharing of data between the most similarly coordinate-valued cells.

(Here’s the executable and sourcecode if you want to run it yourself. You’ll need a Mac made within the past five years.)

So there it is. The Pythagorian formula is a natural consequence of using discrete-state values to build a dynamic “world” in which data can propagate across the system. And once you have Pythagorian distances, you have a true Cartesian coordinate system, and a Euclidean geometry.

It Wasn’t There Again Today

So what, then, is “non-Euclidean” geometry? My personal suspicion is that it’s nothing but a huge exercise in the logical fallacy of equivocation.

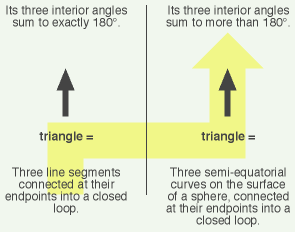
Case in point: What’s the most well-known example of non-Euclidean geometry? It’s geometry on a sphere. Draw a line on a sphere, and it goes all the way around the sphere and reconnects with itself. Any two such lines must intersect (and do so at two points) — there is no such thing as parallel lines. And all triangles have interior angles totalling more than 180° — the bigger the triangle, the larger the total of its three interior angles.

But wait a minute. Did “Euclidean” geometry ever claim that two equatorial circles on a sphere can be non-intersecting? No, it didn’t! In fact, it requires them to intersect at two points. Did “Euclidean” geometry ever say that three semi-circular arcs, connected at their endpoints, have interior angles totalling exactly 180°? No, it did not. It predicts that such a structure will have more than 180° as the sum of its interior angles.

The illusion of a “non-Euclidean” geometry is created simply by shuffling the terms around and then pretending they still mean what they did before you shuffled them. For example, if you redefine the word “line” to mean an equatorial circle on a sphere, then you note that any two such “lines” must intersect, and next you pretend that the word “line” still means what it did before you redefined it, then you discover a system in which two lines can’t be parallel! Wow. Can this really be a serious branch of mathematics?

Time to fire up my trusty equivocation diagram:

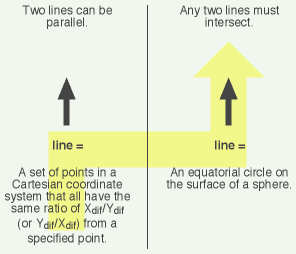
Here’s the same thing for “triangle:”

And this is not just the case with geometry-on-a-sphere. It’s the whole “non-Euclidean” game. Take a set of internally consistent formulas from “Euclidean” geometry, shuffle the terms around in a carefully consistent way, and guess what: The formulas don’t develop inconsistencies they didn’t have before — because you didn’t change the formulas! You changed just the names of the entities to which they refer.

Or, you can change one of the starting axioms — say, change one-parallel-line-through-a-point-near-another-line, to zero-parallel-lines-through-a-point-near-another-line — develop your geometry rules from there, and you don’t find any inconsistencies. Hey, that’s not just term shuffling! Doesn’t that prove something interesting?

Um, no. If you had found any inconsistencies, then the aforementioned geometry-on-a-sphere (which has no parallel “lines”) would be inconsistent. But since we know that geometry-on-a-sphere is completely consistent — seeing as how it’s really perfectly “Euclidean,” taking into account that it is on a “Euclidean” sphere — then we know no inconsistencies will be found. (Please, tell me I’m not the first person to notice this!)

Why?

Why have the mathematical branches of academia been teaching “non-Euclidean” geometry for so long, and treating it as such an important discovery?

I can only guess, but my personal hunch is that it’s a lot more fun to teach a subject that seems mysterious and incomprehensible than it is to teach another class in plain, old, “Euclidean” geometry. Students look up to their teachers as ultra-wise gurus when the subject they are expected to learn is so nonsensical that it seems to baffle the human brain’s ability to visualize it. Just don’t ask the professor how he visualizes it. He doesn’t. There’s nothing to visualize.

And let’s not forget that in order to earn tenure (without which you will be summarily fired at some point in the not-too-distant future), as a professor you are required to come up with a new, original school of thought. If there don’t happen to be any impressive, new schools of thought available to be discovered right now, then you have to make one up, pronto. Or go back to ditch-digging with the rest of us.

Oh, and don’t forget to present your mind-warping, new school of thought with the utmost seriousness. That goes a long way in academia.

prev     next